Ar a 1,05 bar e 300 K entra em um compressor operando em regime permanente, com uma vazão volumétrica de , sai a 12 bar e 400 K. A transferência de calor entre o compressor e sua vizinhança ocorre a uma taxa de 2 kW. Admitindo o modelo de gás ideal para o ar e desprezando os efeitos das energias cinética e potencial, determine a potência de entrada em kW.

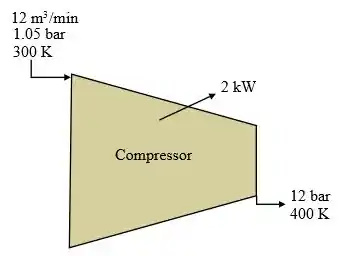
Considere a seguinte equação de balanço de energia para entrada e saída do compressor

Negligenciando as mudanças de energia cinética e potencial, considere a expressão a seguir

Considere a equação do gás ideal como segue:

Substituindo

Calcularemos a taxa de fluxo de massa de ar

Substituindo

Iremos obter a entalpia específica do ar na Tabela A-22 “Propriedades ideais do gás do ar”, do livro texto.

A uma temperatura de 300 k

A uma temperatura de 400 k

Substituindo

O sinal indica que a entrada de energia é fornecida ao compressor.

Portanto, a entrada de energia para o compressor é de