Ar a , e um número de Mach de e forcado a girar para cima em uma rampa que faz um angulo de para fora da direção de fluxo. Como resultado, forma-se um choque obliquo fraco. Determine o angulo da onda, o número de Mach, a pressão e a temperatura após o choque.
Passo 1
Vamos lá! A questão nos afirma que o ar que flui a um determinado número supersónico Mach é forçado a virar para cima por uma rampa, e formas de choque oblíquas fracas. O ângulo de onda, o número de Mach, a pressão e a temperatura após o choque devem ser determinadas.
Podemos representar como,
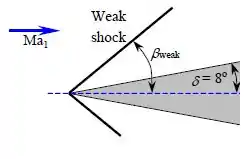
Assumindo que:
- O fluxo é constante.
- A camada limite na cunha é muito fina.
- O ar é um gás ideal com aquecimento específico constante.
A razão de calor específica do ar é .
Passo 2
Pronto já temos todas as informações necessárias, vamos para a análise. Desse modo temos que
com base na Assunção #2, tomamos o ângulo de deflexão como igual à rampa, ou seja,. Então os dois valores do ângulo de choque oblíquo são determinados a partir
que está implícito em . Portanto, resolvemo-lo através de uma abordagem iterativa ou com um solucionador de equações como o EES. Dá e . Então o número de Mach "normal" a montante torna-se
Passo 3
Além disso, os números normais de Mach a jusante tornam-se
A pressão e a temperatura a jusante para cada caso são determinadas como
Passo 4
O número de Mach a jusante é determinada como
Note que são supersónico e é subsónico. No entanto, é supersónico através do choque oblíquo fraco (é subsónico através do choque oblíquo forte).