Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 149
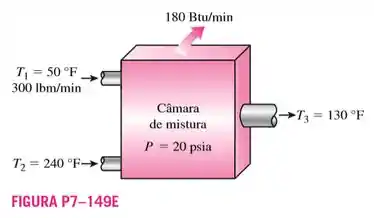
149. Água a e entra em uma câmara de mistura a uma taxa de , onde é misturada em regime permanente com vapor, que entra na câmara a e . A mistura deixa a câmara a e , e calor é perdido a uma taxa de para o ar da vizinhança, cuja temperatura é de . Desprezando as mudanças nas energias cinética e potencial, determine a taxa de geração de entropia durante esse processo.
Passo 1
Olha só! Inicialmente, para se resolver esse problema, vamos destacar alguns pontos importantes que podemos perceber em nosso enunciado...
A primeira coisa perceptível, é que em nosso sistema, existem condições operacionais estáveis. Portanto esse nosso processo, é um processo de fluxo constante. De modo que...
A segunda coisa importante, é que não há interações de trabalho envolvidas.
E a terceira, é que a influência das energias cinética e potencial no nosso sistema são desprezíveis.
Passo 2
Terminada essa parte introdutória, que é chatinha, mas extremamente importante bora por a mão na massa de verdade.
Tomamos a câmara de mistura como sistema. Este é um volume de controle, pois a massa cruza a fronteira do sistema durante o processo.
Observamos que existem duas entradas e uma saída. Sob as premissas e observações declaradas, os balanços de massa e energia para este sistema de fluxo constante podem ser expressos na forma de taxa da seguinte forma...
Para o balanço de massa:
Só que definimos antes que...
E ficamos com...
Passo 3
Continuando nosso raciocínio, bora partir pro balanço de energia...
Mas como estamos em regime permanente...
E ficamos com...
Lembrando que é perdido calor durante o processo, hein!?
Subsituindo em :
Passo 4
Agora, vamos olhar a nossa referência bibliográfica para descobrir as propriedades em cada estado...
E aqui estão elas...
Sabendo que...
E das relações de estado acima, obtemos que...
Passo 5
Pra finalizar, bora partir então, pra análise da taxa de entropia.
A temperatura quando o calor é perdido, está em . Temos que passa-la pra ...
Sendo assim, nossa resposta vai ser dada por...
E pronto! Temos a nossa taxa de geração de entropia...
A entropia é gerada durante esse processo a uma taxa de . Essa geração de entropia é causada pela mistura de duas correntes de fluido (um processo irreversível) e pela transferência de calor entre a câmara de mistura e o ambiente através de um processo finito. diferença de temperatura (outro processo irreversível).