Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 150
150. Vapor deve ser condensado no lado do casco de um trocador de calor a . Água de resfriamento entra nos tubos a a uma taxa de , saindo a . Considerando que o trocador de calor está bem isolado, determine (a) a taxa de transferência de calor no trocador de calor e (b) a taxa de geração de entropia no trocador de calor.
Passo 1
Olha só! Inicialmente, para se resolver esse problema, vamos destacar alguns pontos importantes que podemos perceber em nosso enunciado...
A primeira coisa importante, é que existem condições operacionais estáveis.
Segundo, o trocador de calor é bem isolado, de modo que a perda de calor para o ambiente é insignificante e, portanto, a transferência de calor do fluido quente é igual à transferência de calor para o fluido frio.
Terceiro, alterações nas energias cinética e potencial das correntes de fluido são desprezíveis.
Quarto, as propriedades do fluido são constantes.
Passo 2
Terminada essa parte introdutória, que é chatinha, mas extremamente importante bora por a mão na massa de verdade.
O calor específico da água é igual a
A entalpia e a entropia de vaporização da água a valem...
Tomamos o lado do tubo do trocador de calor onde a água fria está fluindo como o sistema, que é um volume de controle. O balanço de energia para este sistema de fluxo constante pode ser expresso na forma de taxa como...
Mas como estamos em regime permanente...
E ficamos com...
Lembrando que há uma potência de entrada nesse processo, hein!?
Só que...
O que nos leva à...
é a temperatura de saída, de . E é a temperatura de entrada, de . Sendo assim, ficamos com...
Observando que o ganho de calor pela água é igual à perda de calor pelo vapor de condensação, a taxa de condensação do vapor no trocador de calor, que é a nossa potência de entrada, é determinada a partir de...
Passo 3
b) A taxa de geração de entropia no trocador de calor é determinada aplicando a forma da taxa do balanço de entropia em todo o trocador de calor:
Para isso, bora prestar atenção na figura abaixo...
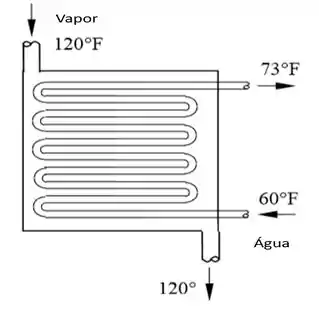
Uma vez que a água é uma substância incompressível e o vapor muda de vapor saturado para líquido saturado, a taxa de geração de entropia é determinada como sendo igual à...
E pronto! Temos a nossa taxa de geração de entropia...
Resposta
a)
b)