Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 153
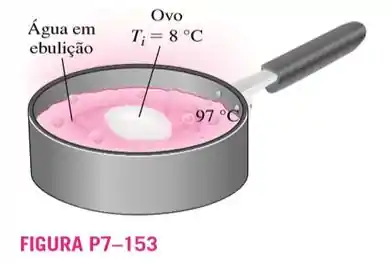
153. Um ovo comum pode ser modelado como uma esfera de de diâmetro. Um ovo inicialmente a uma temperatura uniforme de é colocado em água fervente a . Considerando que e são as propriedades do ovo, determine (a) a quantidade de calor transferido ao ovo até o momento em que sua temperatura média atinge e (b) a quantidade de geração de entropia associada a esse processo de transferência de calor.
Passo 1
Olha só! Inicialmente, para se resolver esse problema, vamos destacar alguns pontos importantes que podemos perceber em nosso enunciado...
Primeira coisa importante... O ovo é de formato esférico com um raio de .
Segundo, as propriedades térmicas do ovo são constantes.
Terceiro, a absorção ou liberação de energia associada a qualquer alteração química e / ou de fase no ovo é insignificante.
E por último... Não há mudanças nas energias cinética e potencial.
Passo 2
Terminada essa parte introdutória, que é chatinha, mas extremamente importante bora por a mão na massa de verdade.
O calor específico do aço é igual a
Já a sua densidade vai valer...
Tomamos uma única esfera de rolamento como sistema. O balanço energético deste sistema fechado pode ser expresso como...
Mas como estamos em regime permanente...
E ficamos com...
Lembrando que há uma energia de entrada nesse processo, hein!?
Só que...
O que nos leva à...
Desconsiderando a potência e levando em consideração apenas a energia, ficamos com...
A massa do ovo é dada por:
De modo que a quantidade de energia na entrada valer...
Passo 3
Novamente, tomamos o ovo como sistema. A entropia gerada durante esse processo pode ser determinada aplicando uma balança de entropia em um sistema estendido que inclua a bola e seus arredores imediatos, de modo que a temperatura do sistema estendido esteja sempre a :
Desconsiderando, o formato de taxa...
A variação de entropia do sistema é dada por...
Desse modo, a entropia gerada vai ser...
Pronto! Essa é a entropia gerada por ovo!