Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 154

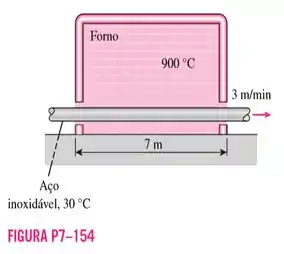
154. Barras de aço cilíndricas e longas ( ρ =     7.833   k g / m 3   e   c p   =   0,465   k J / k g ⋅ ° C ) de 10   c m de diâmetro sofrem um tratamento térmico ao passarem a uma velocidade de 3   m / m i n em um forno de 7   m de comprimento mantido a 900   ° C . Considerando que as barras entram no forno a 30   ° C e saem a 700   ° C , determine (a) a taxa de transferência de calor para as barras no forno e (b) a taxa de geração de entropia associada a esse processo de transferência de calor.

Passo 1

Olha só! Inicialmente, para se resolver esse problema, vamos destacar alguns pontos importantes que podemos perceber em nosso enunciado...

A primeira coisa importante, é que as propriedades térmicas das barras de aço são constantes.

Segundo, as mudanças de energia cinética e potencial das bolas são desprezíveis.

Passo 2

a) Terminada essa parte introdutória, que é chatinha, mas extremamente importante bora por a mão na massa de verdade.

O calor específico das barras aço é igual a

c p = 0,465   k J / k g ⋅ K

Já a sua densidade vai valer...

ρ b a r r a = 7833   k g / m 3

Observando que as hastes entram no forno a uma velocidade de 3   m / m i n e saem na mesma velocidade, podemos dizer que uma seção de 3   m de comprimento da haste é aquecida no forno em 1 minuto. Então a massa da barra aquecida em 1   minuto é...

m b a r r a = ρ b a r r a V b a r r a

m b a r r a = ρ b a r r a l b a r r a A b a r r a

m b a r r a = ρ b a r r a l b a r r a A b a r r a

m b a r r a = 7833   k g / m 3 3   m π 0,1   m 2 4

m b a r r a = 184,6   k g

Em seguida, tomamos a seção de 3   m da barra no forno como sistema. O balanço energético deste sistema fechado pode ser expresso como...

E ˙ e n t r a d a - E ˙ s a í d a = ∆ E ˙ s i s t e m a

Mas como estamos em regime permanente...

∆ E ˙ s i s t e m a = 0

E ficamos com...

E ˙ e n t r a d a = E ˙ s a í d a

Lembrando que há uma energia de entrada nesse processo, hein!? Trabalhando apenas com energia, e não mais com potência, temos que...

m b a r r a h 1 + Q e n t r a d a = m b a r r a h 2

Q e n t r a d a = m b a r r a ( h 2 - h 1 )

Só que...

h 1 = c p T 1

h 2 = c p T 2

O que nos leva à...

Q e n t r a d a = m b a r r a c p T 2 - m b a r r a c p T 1

Q e n t r a d a = m b a r r a c p ( T 2 - T 1 )

De modo que a quantidade de energia na entrada pra barra vai valer...

Q e n t r a d a = ( 184,6   k g ) ( 0,465   k J / k g ⋅ K ) ( 70 0   ° C - 3 0   ° C )

Q e n t r a d a = 57512   k J

Agora, voltemos a trabalhar com potência... Sabendo que as barras passam a uma velocidade de 3   m / m i n , a potência de entrada Q ˙ e n t r a d a vai ser dada por...

Q ˙ e n t r a d a = 57512   k J 60   s  

Q ˙ e n t r a d a = 958,5   k J

Passo 3

b) Novamente tomamos a seção de 3   m de comprimento da haste como sistema. A entropia gerada durante esse processo pode ser determinada pela aplicação de uma balança de entropia em um sistema estendido que inclua a haste e seu entorno imediato, de modo que a temperatura limite do sistema estendido esteja sempre a 900   °   C :

S ˙ e n t r a d a - S ˙ s a í d a ⏟ T a x a   d e   e n t r o p i a   l í q u i d a   t r a n s f e r i d a   p o r   c a l o r   e   m a s s a + S ˙ g e r a d o ⏟ T a z a   d e   g e r a ç ã o d e   e n t r o p i a = ∆ S ˙ s i s t e m a ⏟ T a x a   d e   v a r i a ç ã o d e   e n t r o p i a

S ˙ e n t r a d a - S ˙ s a í d a + S ˙ g e r a d o = ∆ S ˙ s i s t e m a

Desconsiderando, o formato de taxa...

S e n t r a d a - S s a í d a + S g e r a d o = ∆ S s i s t e m a

Q e n t r a d a T e n t r a d a + S g e r a d o = ∆ S s i s t e m a

S g e r a d o = ∆ S s i s t e m a - Q e n t r a d a T e n t r a d a

A variação de entropia do sistema é dada por...

∆ S s i s t e m a = m b a r r a ( s 2 - s 1 )

∆ S s i s t e m a = m b a r r a c p ln ⁡ T 2 T 1

∆ S s i s t e m a = ( 184,6   k g ) ( 0,465   k J / k g ⋅ K ) ⋅ ln ⁡ 70 0 + 273   K 3 0 + 273   K

∆ S s i s t e m a = 100,1   k J / K

Desse modo, a entropia gerada vai ser...

S g e r a d o = ∆ S s i s t e m a - Q e n t r a d a T e n t r a d a

S g e r a d o = 100,1   k J / K - 57512   k J 900 + 273   K

S g e r a d o = 51,1   k J / K

Para passar essa entropia para a forma de taxa, basta dividir a entropia gerada pelo tempo que as barras demoram pra passar, de 1   minuto...

S ˙ g e r a d o = 51,1   k J / K 60   s

S ˙ g e r a d o = 0,85   k W / K

Resposta

a)

Q ˙ e n t r a d a = 958,5   k J

b)

S ˙ g e r a d o = 0,85   k W / K

Ver Outros Exercícios desse livro