Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 10.Problemas - Ex. 46
46- Um escoamento de vapor d’água, com vazão de , a e deve ser resfriado até que a temperatura atinja através do borrifamento de água líquida a e .
Sabendo que o processo deve ocorrer em regime permanente e que a temperatura do meio é igual a , determine a taxa de geração de irreversibilidade no processo.
Passo 1
E aí meus alunos vamos fazer essa questão para mandar um 10 na prova e nos deixar orgulhoso?
Aluno:
Não seja preguiçoso, RAPAAAAZ vamos à luta por que nosso sucesso não se constrói sozinho
Primeiramente vamos pensar, hmm, temos que resfriar vapor d’água que está com uma vazão de a e com água líquida que está a e temperatura de até um ponto onde temos água a
Então vamos desenhar o que está sendo representado, já que tudo fica melhor com desenhos não é mesmo
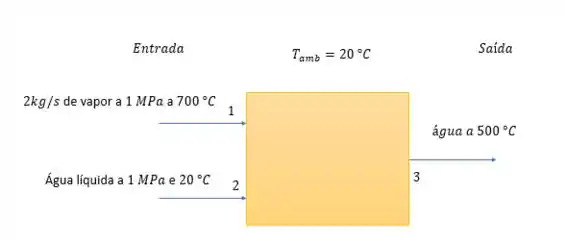
Show de bola! Assim acho que a questão ficou mais clara, a questão nos pede a irreversibilidade e para isso sabendo que o calor jogado no ambiente é nulo então:
O que nos dá uma irreversibilidade de:
Mas como não temos os escoamentos para cada ponto então devemos saber que:
Então vamos coletar os dados de entalpia e entropia dos estados que tanto precisamos
Passo 2
No escoamento 1 que temos vapor a a temos as seguintes propriedades pela tabela
Agora no escoamento que temos água líquida a e pela tabela
Agora os dados para o estado onde temos água a e sabendo que a água se mantém a , pela tabela teremos:
Passo 3
Sabendo que pela equação da continuidade temos:
Então pelas entalpias nós encontramos escoamentos de água iguais a:
Se aplicarmos a equação em teremos:
Passo 4
Maneiro! Agora aplicando os valores na fórmula da irreversibilidade nós teremos:
Com , então:
Fazendo essa singela conta:
E agora eu espero que você tenha saído do modo preguiça pro modo herói
Até a próxima meus alunos!