Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 6.Problemas - Ex. 134
134- A storage tank contains liquid and vapor by volume of liquified natural gas (LNG) at , as shown in . It may be assumed that LNG has the same properties as pure methane. Heat is transferred to the tank and saturated vapor at flows into the steady flow heater which it leaves at .
The process continues until all the liquid in the storage tank is gone. Calculate the total amount of heat transfer to the tank and the total amount of heat transferred to the heater.
Passo 1
Essa é outra daquelas questões que simplesmente eu não puder ver na versão digitalizada do livro, por que simplesmente pulou-se a página hahaha então tiver que pegar da versão original em inglês. Se tiver alguma coisa que não bate com a sua questão please, nos mande mensagem bora se falar!
YEAH MURICA!
Então vamos para a questão (vou tentar ser bem descritivo aqui para que você possa verificar se está batendo com o livro ou não)
Inicialmente temos gás natural (que pode ser aproximado para metano) com na sua forma líquida e na sua forma em vapor em um tanque de a
E parou aqui, vamos coletar as propriedades dessa água na tabela para que nós tenhamos mais segurança no decorrer da questão
Pelos dados da tabela temos as seguintes um volume específico pro metano de e um volume específico para o vapor de para uma temperatura de :
Ok, você pode ter olhado para isso e deve ter surgido um grande ‘?’ na sua cabeça
Então, o que temos aqui é uma porcentagem de em volume de para o líquido de metano e de gás, e se fizéssemos a conta:
Nós estamos considerando que da massa dentro do tanque é composta por líquido, o que não é a verdade, então temos que multiplicar pelas suas proporções (já que massa e volume são proporcionais)
Então temos no estado inicial de metano líquido e de metano em seu estado gasoso e com isso a massa total de metano será de
Passo 2
Como queremos saber o calor produzido pelo tanque e o calor transferido para o aquecedor nós também teremos que pegar os valores de energia interna e da entalpia nesse tanque e para isso temos
Desenhando aqui a questão para que você entenda melhor o que está acontecendo
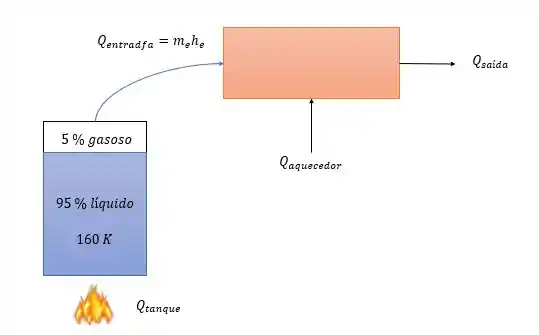
Dessa forma o calor transferido ao tanque pode ser modelado como:
Aqui não pense em massa líquida e massa gasosa, pense em massa do estado inicial e final (a massa do estado inicial por exemplo é de que é a massa total) e como temos mais massa no estado final que no inicial então a parcela é positiva
Então vamos achar a massa no estado 2, sabendo que no estado final somente temos vapor no tanque (100 % de vapor):
Então a massa escapada será de:
Sabendo que pois sai do tanque somente vapor
Passo 3
Porém como temos dois estados no estado inicial então a parcela também pode ser calculada como:
Então o calor fornecido ao tanque será de:
Bastante calor! Qualquer dúvida verifique os valores e não deixe de contar com a gente
Passo 4
Agora para o calor transferido ao aquecedor sabendo que na saída temos uma temperatura de metano a de vapor em uma pressão igual a pressão de saturação de que é de (o que vamos aproximar para )
Pela tabela vemos que nessas condições a entalpia é de
Dessa forma o calor transferido ao aquecedor é de:
Como a massa que flui no aquecedor é a aproximadamente a mesma e igual a
Então:
Também muito calor transferido, valores industriais são fortes assim mesmo.
E o bagulho é loco, até a próxima questão para mais loucuras