Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 9.Problemas - Ex. 66
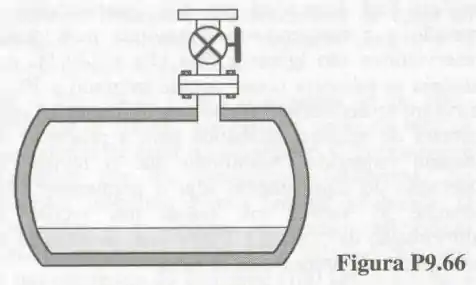
66- A mostra um tanque rígido, com volume interno de , que contém de a temperatura ambiente .
Uma válvula situada no topo do tanque é, então, aberta e vapor saturado é estrangulado até e descarregado num coletor.
Durante esse processo, a temperatura interna do tanque permanece constante e igual a . A válvula é fechada quando não existe mais líquido no tanque.
Nestas condições, determine o calor transferido ao tanque e a variação líquida de entropia no processo
Passo 1
Sua prova é amanhã? E você sente como se tudo tivesse perdido? No mais profundo vazio do universo?
Vem comigo que sua alta estima vai lá pra lua! Pois o céu é o limite e você foi feito para atravessar os céus!
Para te tirar desse desespero vamos começar pelo começo, anotando os estados do que está nesse tanque:
Estado inicial ou estado :
E pela tabela temos as seguintes propriedades:
E como nos foi dada a massa e o volume que ela ocupa, então podemos dizer que o volume específico do no estado inicial é de:
E isso nos diz que temos uma certa titulação pro (já que , ou seja, que tem dois estados dentro do tanque e que será dada por:
Com isso podemos achar todas as outras propriedades:
E para a energia interna, bem como a tabela não nos ajuda em dar os valores vamos ter que fazer:
E como a válvula é aberta fazendo com que a parte em vapor saia, então temos que pegar o valor da entalpia desse gás que sai do tanque para o coletor (que é vapor)
Passo 2
Agora que coletamos tudo que é preciso coletar do estado inicial, vamos de outros estado do que está em vapor saturado a e em um coletor de modo que não temos mais nenhum líquido no tanque, somente gás no coletor.
Aqui pode entrar um ponto de desistência, pois quais informações eu tenho para prosseguir? Se não sei temperatura e nem nada além da pressão.
Lembra que eu disse no passo anterior que o gás é vazado como gás saturado do tanque e que eu preciso da entalpia de vapor, então essa entalpia que vai ser a entalpia do gás no estado do gás de saída e que sai a , da seguinte forma
Então pela tabela conseguimos tirar para e
Esses são os valores de propriedade do gás que escapa do tanque
Não vale muito a pena pegar o volume específico aqui, pois não temos o volume do coletor para dizer quanto vale sua massa. Precisamos saber do estado final do gás para isso
Passo 3
E aí sim temos o estado final do que é de vapor saturado, que tem as seguintes propriedades
O que nos dá uma massa de:
Isso nos dá uma massa escapada de:
Passo 4
Agora podemos começar a responder a questão, começando por quanto de calor é fornecido ao tanque para que toda o evapore:
Sabendo que o calor é relacionado ao quanto de variação de energia interna variou no estado inicial e final somada com a entalpia do transporte do gás de um lado pro outro nós temos:
Bastante calor para isso acontecer
E a geração de entropia será dada por:
E assim derrotar o vazio e poder rasgar os céus que é o nosso limite
