Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 9.Problemas - Ex. 78
78- Uma pequena barragem descarrega de água a e através de uma tubulação horizontal que apresenta diâmetro igual a .
Esta tubulação está conectada a linha vertical de alimentação de uma turbina hidráulica. Esta linha apresenta diâmetro igual a . A turbina está posicionada a abaixo da tubulação que apresenta diâmetro igual a .
Admitindo que os escoamentos de água são adiabáticos e reversíveis, determine a pressão na seção de alimentação da turbina. Considerando que a pressão na seção de descarga na turbina é igual a , determine a potência da turbina
Passo 1
Esse é aquele tipo de questão que pede um desenho né? Por que tem bastante coisa aí sendo descrita
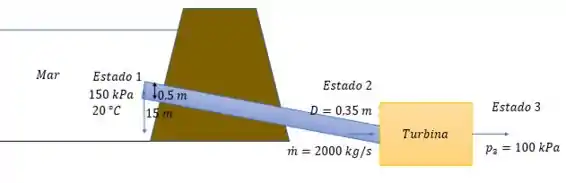
Onde se pede a pressão no estado e a potência da turbina.
Nesse caso temos mais do que variação de pressão para considerar para energia na turbina e sim a energia potencial e a cinética, então arregace as mangas por que aqui tem trabalho!
A água líquida a tem um volume específico de e esse volume específico se mantém constante em toda a trajetória.
Primeiramente vamos descobrir a velocidade da água nos estados e simplesmente pela vazão e que tem fórmula de:
Então a velocidade da água no estado será:
E a velocidade da água no estado será:
Passo 2
Agora podemos aplicar a equação de Bernoulli que é extremamente famosa no mundo da Engenharia por resolver grande parte das questões de líquidos incompressíveis, cujo um desses líquidos é um líquido chamado água. Que é muito vital para nós seres humanos.
Por Bernoulli temos:
Sabendo que então:
Então a pressão que chega no estado , que é a entrada da turbina é de:
Multiplique a pressão por para achar o valor em se não dá um erro um tanto chato de entender
Passo 3
Agora a potência da turbina será dada por:
De até pois o trabalho considera a energia que vai desde o estado inicial até o estado final então temos que considerar todo o circuito de energia.
Então supondo que a velocidade no estado é praticamente nula (pois a turbina absorveu grande parte da cinética e deixou somente a água inundar a parte depois dela) nós temos:
E essa será a potência que a turbina exerce. Espero que essa questão tenha te ajudado, até a próxima!