Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 12.Problemas - Ex. 79
79- Um aquecedor residencial de alta eficiência opera com um trocador de calor ar-ar. O trocador é alimentado com ar de retorno do ambiente e pré-aquece de ar proveniente do meio externo (temperatura igual a e umidade relativa de ).
Qual a quantidade de água que deve ser adicionada ao ar externo se a temperatura e a umidade relativa do ar a ser injetado no ambiente condicionado forem, respectivamente, iguais a e ?
Passo 1
Estamos aqui para lançar o novo aquecedor mega blaster 3000 e a equipe de marketing precisa do valor da quantidade de água a ser adicionada para poder fazer uma boa chamada do produto
E nós como projetistas temos que dar essa resposta e aí o produto ser um baita sucesso comercial e todo mundo poder ficar feliz com isso
Uma boa para poder resolver essa questão é fazer um desenho do que está sendo dito então vamos lá, eu vou desenhar primeiro e explicar o que está sendo dito depois
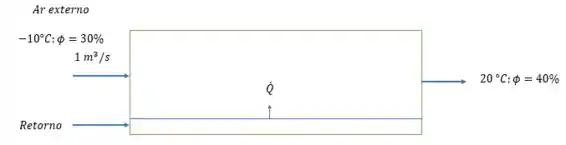
Ou seja, o ar de retorno faz com que o ar externo esquente mais rapidamente, o que faz manter a temperatura interna ficar mais estável em um determinado valor e isso fica mais fácil adicionando água pois ela é mais fácil de esquentar que o ar, na real não precisamos nos preocupar com esse retorno na questão e sim em com a entrada e a saída de ar.
Os dois ambientes, tanto interno (de saída) e externo (de entrada) estão a pressão atmosférica que é arredondada para
Começando pelas propriedades do ar úmido externo, a pela tabela teremos uma pressão de água igual a:
E como temos de umidade relativa então a pressão de vapor da água será menor ainda
Então a pressão de ar na entrada será de:
E a vazão mássica de ar na entrada será de:
E para fechar a coletânea de propriedades para a seção de alimentação vamos calcular a umidade absoluta que será:
Passo 2
Agora para o estado interno que é o ar que está a e com , nesse estado a pressão da água será e com isso a pressão do vapor da água no ar será de:
E a umidade absoluta desse ar na saída será:
Essa medida é importante e vamos entender no próximo passo por que
Passo 3
E nosso objetivo não é calcular o quanto de massa de água foi adicionada pelo ar condicionado? Então, como a massa de ar não muda então podemos fazer o seguinte:
Pois não é a razão entre a massa de água e a massa de ar, então se pegarmos a diferença entre o estado final do ar com o estado inicial da umidade absoluta e multiplicarmos pela massa de ar nós teremos a massa de líquido. Então fazendo isso nós temos:
E assim nosso produto foi um sucesso comercial pois a nossa equipe comercial é boa demais
