Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 7.Problemas - Ex. 85
85- Uma jarra com de leite a é colocada num refrigerador de Carnot e é então resfriada até . A temperatura do reservatório de alta temperatura do refrigerador é igual a e as propriedades do leite podem ser consideradas iguais as da água líquida. Determine o calor transferido do leite e também o trabalho necessário para acionar o refrigerador neste processo.
Passo 1
Alô meus consagrados, tudo bem como vocês? Vamos fazer essa questãozinha marota.
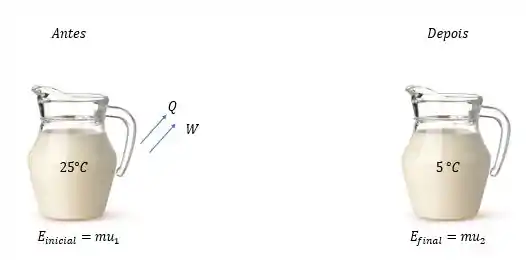
E aqui temos o seguinte modelo de energia para a jarra do leite
A energia interna inicial do leite vai diminuindo conforme o tempo passa, pois uma parcela de calor é retirada do leite e ainda teríamos um possível trabalho do leite para o ambiente e nesse caso aqui esse trabalho é nulo, portanto o modelo de energia pro leite seria
Passo 2
Primeiramente vamos encontrar a massa contida no jarro de leite sabendo que ela pode ser calculada como:
E sabendo que as propriedades do leite são parecidas com a da água (pela própria questão) então a pela tabela temos o volume específico de:
Então a massa inicial será de:
E como não há uma diferença significativa do volume específico do leite nas duas temperaturas então vamos considerar essa massa aí mesmo como constante.
Não esqueça de usar medidas no SI, ou seja
Agora pela mesma tabela temos que a energia interna do leite a é de e a é de
Então o leite perde um calor de:
Lembrando que esse calor é perdido para a geladeira
Com isso respondemos a primeira questão
Passo 3
Agora queremos saber o trabalho exercido pela geladeira, sabendo que a temperatura da fonte quente do refrigerador é de e que pelo menos a temperatura do ambiente da geladeira tem que estar a para fazer com que o leite esteja nessa temperatura, então o coeficiente de refrigeração da geladeira deverá ser de:
Onde essas temperaturas deverão estar em , então:
E isso nos dá um trabalho de:
Onde esse calor é justamente o calor que é retirado do leite, pois esse calor é retirado por causa de alguma coisa né? E essa alguma coisa é trabalho do refrigerador, logo:
E é isso galerinha, até mais!