89- Uma bomba de calor deve ser utilizada para aquecer uma residência no inverno e depois, funcionando em operação reversa, para resfriar a residência no verão.
A temperatura interna deve ser mantida a no inverno e no verão. A transferência de calor, através das paredes e do teto é estimada em por horas e por grau de diferença de temperatura entre o meio interno e externo da residência.
- Se a temperatura externa no inverno é , qual é a potência mínima necessária para acionar a bomba de calor?
- Se a potência fornecida ao ciclo é a mesma do item a qual é a temperatura máxima externa (no verão) para que a temperatura interior da residência ainda possa ser mantida a ?
Passo 1
Vamos começar a questão dentro de estejam em suas marcas que vamos fazer a contagem regressiva`

Pananana pananananaaaaa panana pananananananaaaaa
Aiai, vamos para o que é dito no enunciado da letra .
Fazendo o esboço dela temos:
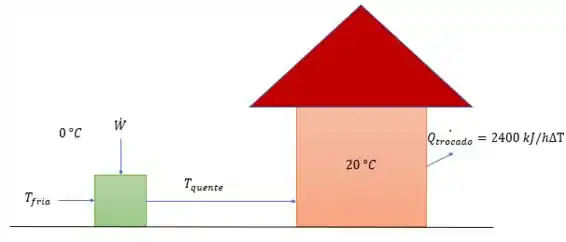
Onde consideramos a bomba uma bomba de Carnot, e aqui queremos saber a potência da bomba com:
Então o rendimento dessa bomba que é de:
Porém o rendimento em uma bomba de calor também pode ser escrito como:
E como queremos a potência mínima da bomba para que o sistema funcione, então o calor fornecido pela fonte quente deve ao menos igualar a troca de calor entre a casa e o ambiente e como o calor trocado entre a casa e o ambiente é em por hora por variação de temperatura entre o lado de dentro e o lado de fora então:
Já que
Logo:
E essa é a resposta da letra
Passo 2
Agora para a letra a bomba será uma bomba de resfriamento, então queremos tirar calor da casa sabendo que é a mesma da letra anterior
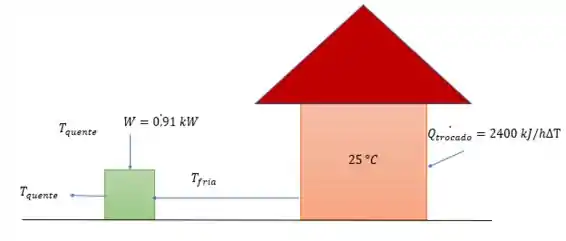
Supondo que temos a mesma bomba de Carnot com:
E cuja eficiência de refrigeração é em relação a temperatura fria enquanto a bomba de calor é referente a temperatura e calor quente, ou seja:
Substituindo as coisas que conhecemos já, nós teremos:
Aqui fizemos a conversão de para que é uma medida mais aceitável.
Fazendo essa conta nós encontramos:
Po, preciso dessa bomba aí hahahah falo isso por que faço essa questão um dia depois de ter batido onde moro e nossa que insuportável que ficou