Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 6.Problemas - Ex. 132
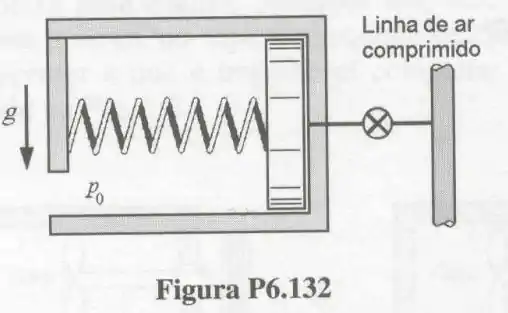
132- Um conjunto cilindro-pistão-mola é adiabática e está conectado a uma linha de ar comprimindo e conforme o mostrado na .
Inicialmente, o cilindro está vazio e a tensão na mola é nula. A válvula é, então, aberta e é mantida nesta posição até que a pressão no cilindro atinja .
Formule uma expressão para em função de e a temperatura do ar na tubulação. Admitindo que é igual a , calcule
Passo 1
Note que a questão pede que formulemos uma fórmula para a temperatura no cilindro no seu estado final, então isso tem o cheirinho forte de questão que começa teórica e depois vai para a aplicação, pois depois ele quer o valor dessa temperatura mesmo
Conheçam a página do Facebook Meme-Theoretic Theoretical Physics-Memes, é muito boa apesar deles fazerem memes com uns conceitos super avançados de física, o que é genial hahahah
Show de bola!
Se liga no problema, temos uma linha de ar comprimido que injeta ar comprimido em um cilindro que realiza trabalho por meio de uma mola, então seu modelo de energia é simplesmente
Ou seja, a variação da energia calorífica dentro do cilindro é igual a energia potencial do ar entrante descrida pelo trabalho que o cilindro faz. Mas como o cilindro está vazio no começo então a massa inicial no cilindro é nula, o que nos deixa com:
Beleza, então a próxima coisa que podemos comentar aqui é sobre o trabalho feito pelo cilindro, que será algo como:
Onde não temos e nem no estado inicial do cilindro, então a única coisa que varia nesse cilindro é que no estado inicial a pressão nele vale e no final e o trabalho disso será dada por:
Como um triângulo no diagrama onde varia de até e vai de 0 até , logo a equação da energia fica:
Onde a massa que entra é justamente a massa do ar no cilindro no seu estado final, então cortando
Beleza, demos um passo gigantesco para resolver a questão
Passo 2
Agora começa a entrar os detalhes, pois afinal queremos temperatura e não energia interna e nem entalpia.
Então sabendo que:
E que pela tabela temos e que com , então uma forma de usar essas informações é com
Então a temperatura do cilindro será dada por:
Passo 3
Só que temos que tirar esse da equação, pois não é algo que a questão pede para ter na fórmula e pra isso podemos usar a fórmula de Clapeyron que nos dá para o gás ideal:
Onde:
Sendo e , logo:
Arrumando um pouco as coisas para termos isolado nós temos:
Ufa!
Passo 4
Então substituindo os valores que conhecemos (, nós teremos:
Faça essa conta com tranquilidade que você chega no resultado.
Selo de questãozinha braba, vamos para mais pois um engenheiro gosta desses desafios