Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 7.Problemas - Ex. 95
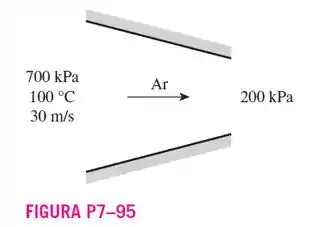
95. Ar é expandido em um bocal adiabático durante um processo politrópico com . O ar entra no bocal a e com uma velocidade de , saindo a uma pressão de . Calcule a temperatura e a velocidade do ar na saída do bocal.
Passo 1
Bora fazer mais uma questãozinha sobre entropia!
Olha só! Esse nosso processo é um processo de fluxo constante, pois não há alterações com o tempo. Além disso, não há transferência de calor ou trabalho no eixo associado ao processo. E o mais importantes... Temos que considerar que o ar é um gás ideal com aquecimentos específicos constantes.
Afinal, praticidade é tudo que a gente quer!
Da tabela , sabemos que as propriedades do ar à temperatura ambiente são...
E a razão específica de calor...
Então, uma vez que todo esse processo pelo qual passa o ar, é dado como reversível e adiabático então ele é um processo isentrópico.
Sendo assim, as relações isentrópicas de gases ideais vão se aplicar.
Passo 2
Bom! Vamos pro que interessa! Para as relações isentrópicas de gases ideais, temos a seguinte equação...
E do enunciado, sabemos que...
é a temperatura na qual o ar está no início do processo. Só que precisamos passar ela de para .
Fácil, né não!? Basta somar com ... Desse jeito aqui:
A pressão vale e a pressão vai valer .
Sendo assim...
Passo 3
Nesse nosso sistema, existe apenas uma entrada e apenas uma saída...
Sendo assim, a variação de massa inicial, que chamaremos de é igual a variação de massa no instante final, de saída.
Ou seja,
E o nosso sistema é um sistema de controle...
Desse modo, vamos expressar o balanço de energia para este sistema de fluxo constante, na forma de taxa...
A questão nos diz que o ar é expandido em local adiabático. Assim, a variação de energia do nosso sistema é igual a zero...
E ficamos com:
Bom! Não temos os valores diretos nem de nem de !
Mas sabemos que eles dois podem ser obtidas a partir das duas fórmulas abaixo...
Desse jeito...
Substituindo os valores numéricos já conhecidos...
Pronto! Essa é a velocidade de saída!