Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 2.Problemas - Ex. 71
Água é bombeada de um lago para um tanque de armazenamento acima com uma vazão de , consumindo de energia elétrica. Desprezando as perdas por atrito nos tubos e todas as variações de energia cinética, determine a eficiência global da moto-bomba e a diferença de pressão entre a entrada e a saída da bomba.
Passo 1
O exercício pede para a gente calcular primeiro a eficiência da bomba. Nós calculamos a eficiência de um equipamento dividindo o resultado desejado pelo consumo necessário.
No caso da bomba, o resultado desejado é o aumento da energia potencial da água do lago por segundo. Ela é elevada do lado até o tanque. Para isso, ela consome de energia elétrica a cada segundo.
O exercício já informou a energia elétrica consumida por segundo .
Só precisamos calcular o aumento de energia potencial da água . Para facilitar o cálculo de , vamos chamar de ponto o ponto onde a água do lago é sugada pela tubulação e de ponto o ponto onde a água é despejada para o tanque.
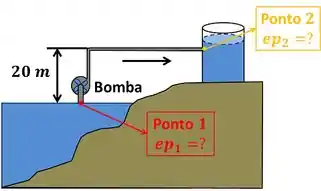
O aumento de energia potencial é a diferença entre o valor da energia potencial que a água passou a ter no ponto e o valor da energia potencial que a água tinha no ponto . As fórmulas das duas estão abaixo.
onde é a aceleração da gravidade e vale .
Vemos que essas energias dependem da altitude que a água tinha no lago e da altitude que a água passou a ter no tanque . Podemos medir a altura da água a partir do ponto . Desse jeito, valeria:
A altitude é informada pelo enunciado.
Além disso, e são as energias potenciais por unidade de massa. Elas são medidas em joule por quilograma .
Isso quer dizer que precisamos achar a quantidade de massa que passa pela bomba a cada segundo para conseguir calcular o aumento de energia total da água. Descobrimos pela fórmula abaixo.
é o volume de água que passa pela bomba a cada segundo. Ele mede segundo o enuciado.
Para converter a quantidade de volume para a quantidade de massa , multiplicamos pela massa específica da água . Atenção! O exercício não fala quanto vale o da água líquida a temperatura ambiente. Mas podemos considerar que ele vale !
A última etapa de cálculo da eficiência da bomba é calcular o aumento de energia potencial da água . A fórmula do aumento de energia potencial da água se encontra abaixo:
O pode ser calculado com a seguinte fórmula:
Agora vamos para o próximo passo de substituição dos valores que temos nas fórmulas que conhecemos.
Passo 2
A vazão da água vale:
As energias potenciais da água são:
Substituindo esses valores na fórmula de aumento da energia potencial, vemos que ela vale:
Convertendo esse valor para quilowatt para ele ficar na mesma unidade de :
Colocando todos esses valores na fórmula de eficiência da bomba , encontramos:
Passo 3
Descobrimos que a bomba entrega de energia a cada segundo para a água. Essa energia que a água ganha é convertida em pressão. Ou seja, a pressão da água aumenta conforme ela passa pela bomba. Por causa disso, existe uma fórmula de aumento de energia da água que depende da variação de pressão da água .
Além disso, o exercício diz que as perdas por atrito e a variação de energia cinética da água são desprezíveis. Isso significa que o aumento de pressão é o único tipo de variação de energia que a água sofre conforme passa pela tubulação e pela bomba. Em outras palavras, o aumento de energia da água, causado pela bomba, vai todo pro aumento de pressão da água .
Por isso, essa outra fórmula de aumento de energia por segundo depende só da diferença de pressão entre a entrada e a saída da bomba e não da variação de velocidade da água. Podemos usar esse fato para achar o valor de que o exercício quer.
Como já sabemos que vale , calculamos reorganizando a fórmula acima.
Já temos todos os valores que precisamos! Agora vamos calcular !