Água escoa através de um medidor Venturi, conforme ilustrado na Fig. P1.36. A pressão da água no tubo suporta colunas de água que diferem de 10 in (0,25 m) de altura. Determine a diferença de pressão entre os pontos a e b, em lbf/in^2. A pressão aumenta ou diminui na direção do escoamento? A pressão atmosférica é de 14,7 lbf/in^2, o volume específico da água é de 0,01604 ft^3/lb (0,001 m^3/kg) e a aceleração da gravidade é g = 32,0 ft/s^2 (9,7 m/s2).
Passo 1
Oiiii, tudo bem?
Vamos lá resolver mais uma questão de termodinâmica! Nessa questão vamos lidar com medidas em unidades inglesas. Então dá uma revisada nelas e vem com a gente fazer essa questão!
Passo 2
O enunciado nos dá alguns parâmetros:
- Altura da diferença das colunas de água:
- Pressão atmosférica:
- Volume específico da água:
- Aceleração da gravidade:
Com todos os parâmetros anotados, vamos seguir para os próximos passos.
Passo 3
O esquemático do problema é o seguinte
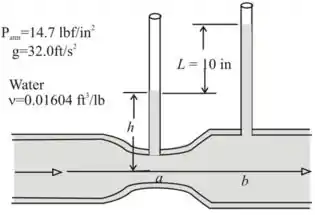
Passo 4
Calculando a densidade da água:
Onde, é o volume específico da água. Substituindo os valores, temos
Passo 5
Calculando a pressão no ponto
Passo 6
Calculando a pressão no ponto
Passo 7
Subtraindo as pressões no ponto do ponto , temos
Assim, como a diferença de pressão entre os pontos e é positiva, a pressão aumenta na direção do fluxo.
Resposta
A pressão aumenta na direção do fluxo.