Construa um gráfico de cada uma das quantidades calculadas no Problema 8.10 em função da pressão no condensador na faixa de 0,3 lbf/in2 a 14,7 lbf/in2. Mantenha a potência líquida constante. Discuta os resultados.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?! Nessa questão a gente vai usar o computador como nosso aliado, vamos usar o software Engineering Equation Solver (EES). Ele é ótimo para os problemas de termodinâmica, e é um dos que o livro recomenda para o estudo.
Passo 2
Primeiro, a gente pode dar uma olhada no diagrama que representa o ciclo de Rankine ideal
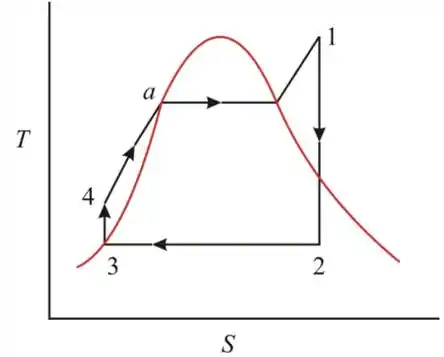
Passo 3
Podemos obter as propriedades na entrada da turbina, com pressão e temperatura das tabelas de vapor superaquecido
Obtendo as propriedades da água a pressão condensada das tabelas de água saturada
Passo 4
Achando o título no estado 2 aplicando a condição isentrópica durante o processo 1-2
Achando a entalpia no estado 2
A entalpia no estado 3 é igual a entalpia de líquido saturado a pressão de
Achando o trabalho da bomba durante o processo 3-4 usando a equação
Passo 5
Achando a entalpia no estado 4 aplicando a equação de energia no processo 3-4
Passo 6
Agora que a gente já tem os dados que precisamos, precisamos fazer alguns cálculos que a questão pede
a) Achando a taxa de vazão mássica do vapor, usando a potência desenvolvida pelo ciclo
Passo 7
b) Achando a taxa de transferência de calor para o fluido em trabalho passando pelo gerador de vapor
Passo 8
c) Achando a eficiência térmica usando equação
Passo 9
d) Achando a taxa de vazão mássica de água resfriando aplicando o balanço de energia no condensador
Aqui, é a entalpia de resfriamento da água na entrada e é a entalpia de resfriamento na saída.
Obtendo esses valores de entalpia usando as tabelas de água saturada em e
Substituindo os valores na equação
Passo 10
Escrevendo o programa para a solução no programa EES
"Dados Iniciais"
p1 = 1400 "pressão na entrada da turbina"
T1 = 1000 "temperatura na entrada da turbina"
"p2 = 2 pressão no condensador"
p3 = p2
x3 = 0
p4 = p1
Wciclo = 1*10^9 "potência de saída do ciclo"
Twin = 60 "temperatura na entrada de água resfriada"
Twout = 76 "temperatura na saída de água resfriada"
"Cálculos nas Tabelas"
h1 = Enthalpy(Steam; P = p1; T = T1)
s1 = Entropy(Steam; P = p1; T = T1)
h2s = Enthalpy(Steam; P = p2; s = s2s)
s2s = s1
h3 = Enthalpy(Steam; P = p3; x = x3)
v3 = Volume(Steam; P = p3; x = x3)
h4 = h3 + v3 * (p4 - p3) * (144/778)
pw1 = Pressure(Steam; T = Twin; x = 0)
hwin = Enthalpy(Steam; P = pw1; x = 0)
pw2 = Pressure(Steam; T = Twout; x = 0)
hwout = Enthalpy(Steam; P = pw2; x = 0)
"Cálculos"
Wciclo = mdot * ((h1-h2s) - (h4-h3))
Qin = mdot * (h1-h4)
eta = Wciclo / Qin
0 = mdot * (h2s-h3) + mdotw * (hwin-hwout)
Passo 11
a) Plotando a taxa de vazão mássica pela pressão
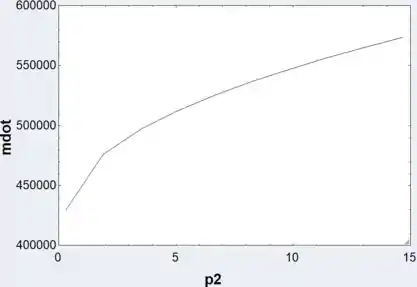
Passo 12
b) Plotando o calor pelo condensador pela pressão
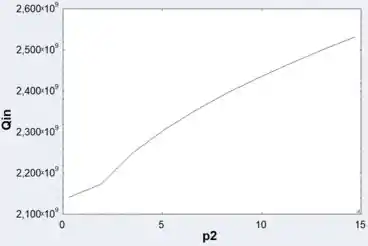
Passo 13
c) Plotando a eficiência pela pressão
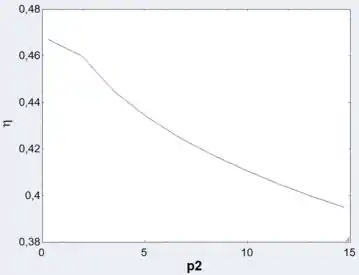
Passo 14
d) Plotando a taxa de vazão mássica de água pela pressão
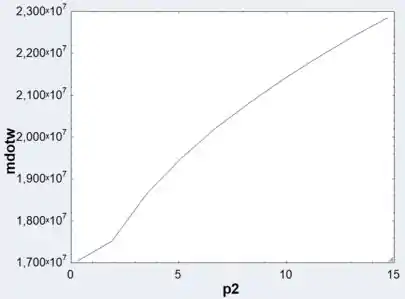
Resposta
Ei, a resposta está no passo a passo :)