Enunciado
Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 8.Problemas - Ex. 36
A água é o fluido de trabalho em um ciclo ideal de Rankine. O vapor entra na turbina a 1400 lbf/in² e 1000°F. A pressão no condensador é de 2 lbf/in². A potência líquida de saída do ciclo é 1 x Btu/h. A água de resfriamento sofre um acréscimo de temperatura de 60°F a 76°F, com queda de pressão desprezível, ao passar pelo condensador. Determine para esse ciclo:
(a) a vazão mássica de vapor, em lb/h.
(b) a taxa de transferência de calor, em Btu/h, para o fluido de trabalho que passa pelo gerador de vapor.
(c) a eficiência térmica.
(d) a vazão mássica da água de resfriamento.
Passo 1
Faaaaaaala galera!!! Tudo certinho? Nessa questão aqui vamos começar esquematizando um ciclo ideal de Rankine:
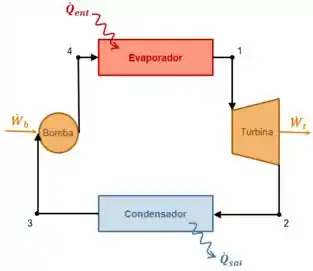
Primeiro vamos expor as hipóteses trabalhadas:
1 – Cada componente do ciclo vai ser analisado como um volume de controle em regime estacionário, com uma entrada e uma saída de fluido.
2 – Todos os processos sobre o fluido de trabalho apresentam reversibilidades internas.
3 – A turbina e a bomba operam adiabaticamente.
4 – Os efeitos das energias cinética e potencial são desprezíveis.
5 – O vapor superaquecido entra na turbina e o líquido saturado sai pelo condensador.
Vamos agora dar uma organizada nos dados:
E com isso já podemos definir as propriedade de cada um dos estados no ciclo!
Vamos fazer no próximo passo.
Passo 2
Vamos começar definindo o estado 1. O que acontece na turbina é um processo isentrópico, então:
No estado 1 temos que a água se encontra no estado de vapor superaquecido a uma pressão de 1400 lbf/in², então pela tabela A-4E na pressão de 1400 lbf/in² a 1000°F:
Show! Já podemos ir para o estado 2.
Passo 3
Temos que no estado 2, a água se encontra a uma pressão de 2 lbf/in² e na forma de uma mistura vapor e líquido! Então vamos voltar para a Tabela A-3E na pressão de 2 lbf/in² e pegar as propriedades que precisamos para o calculo do título dessa mistura:
Beleza! Agora vamos calcular o título da mistura através das entropias específicas:
E para terminar a definição do estado 2, vamos calcular sua entalpia específica !
Pronto! Vamos continuar definindo os outros estados que faltam! Só mais 2, prometo!
Passo 4
Para o estado 3, temos que a pressão é a mesma do estado dois, 2 lbf/in², e que pela hipótese 5 a água está no estado de líquido saturado. Então vamos para a tabela A-3E pegar tudo que temos direito para a água líquida saturada a 2 lbf/in²:
Oba! O estado 3 já está todo definidinho, todo bonito! Vamos partir para o último estado!
Passo 5
O último estado é o 4. Nele podemos calcular a entalpia específica através do trabalho da bomba!
Nós temos que o trabalho realizado pela bomba se dá por:
Onde temos a aproximação da Eq. 8.7b
Ou seja, ficamos com:
Já temos o volume específico, todas as pressões e a entalpia específica do estado 3! Vamos achar a entalpia específica do estado 4!
Finalmente temos todos os estados definidos! Vamos partir para o cálculo das letras da questão!!!
Passo 6
Para a letra (a), podemos achar a vazão mássica do vapor através da fórmula do trabalho do ciclo!
Massa né? Agora é só substituir!
Tranquilo né? Vamos em frente!
Passo 7
Na letra (b) ele nos pede a taxa de transferência de calor, em Btu/h, para o fluido de trabalho que passa pelo gerador de vapor. Esse gerador é o evaporador que fica entre os estados 1 e 4!
Substituindo os dados:
Faltam só mais duas letras!
Passo 8
Já na letra (c) é pedido a eficiência térmica!
Então substituindo tudo, ficamos com:
Moleza né? Faltam só mais uma só, aguenta fime aí!
Passo 9
Para a letra (d) vamos analisar apenas o volume de controle do condensador!
Temos:
Ao mesmo tempo que para a água de resfriamento, que é a água que recebe o calor liberado pelo condensador tem a seguinte equação
Onde, pela tabela A-2E:
Igualando ambas equações ficamos com:
Última parte agora é substituir os dados!!!
Show de bola! Por aqui terminamos!!! Bora pra próxima questão?
Resposta
(a)
(b)
(c)
(d)