Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Moran e Shapiro - Princípios de Termodinâmica para Engenharia- Ed: 7º - Capítulo 8.Problemas - Ex. 20

A água c o fluido de trabalho em um ciclo de Rankine. O vapor superaquecido entra na turbina a 8 MPa e 560°C com uma vazão mássica de 7,8 kg/s e sai a 8 kPa. O líquido saturado entra na bomba a 8 kPa. A eficiência isentrópica da turbina é dc 88% e a eficiência isentrópica da bomba é de 82%. A água de resfriamento entra no condensador a 18°C e sai a 36ºC sem alteração significativa da pressão. Determine:

(a) a potência líquida produzida, em kW.

(b) a eficiência térmica.

(c) a vazão mássica da água de resfriamento, em kg/s.

Passo 1

Saalve, tranquilo?

Vamos resolver juntos mais uma questão de termodinâmica?!

Passo 2

É dado que:

  • Vapor superaquecido entra na turbina com pressão: p 1 = 8   M P a
  • Temperatura superaquecida: T 1 = 56 ° C
  • Taxa de vazão mássica do vapor: m ˙ = 7,8   k g / s
  • Pressão de saída da turbina: p 2 = 8   k P a
  • Líquido saturado entra na bomba a pressão: p 3 = 8   k P a
  • Eficiência isentrópica da turbina: η T = 88 %
  • Eficiência isentrópica da bomba: η B = 82 %
  • Água resfriada temperatura de entrada: t w ,   e n t = 18 ° C
  • Água resfriada temperatura de saída: t w ,   s a i = 36 ° C

O diagrama T - s é mostrado abaixo

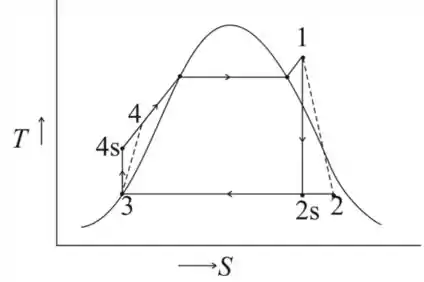
Passo 3

Da tabela de vapor superaquecido com p 1 = 8   M P a e T 1 = 560 ° C

h 1 = 3545,3   k J / k g

s 1 = 6,9072   k J / k g ⋅ K

Da tabela de vapor superaquecido com p 2 = p 3 = 8   k P a

h f = 173,88   k J / k g

h f g = 2403,1   k J / k g

s f = 0,5926   k J / k g ⋅ K

s f g = 7,6361   k J / k g ⋅ K

v f = 1,0084 ⋅ 10 - 3   m 3 / k g

Passo 4

O processo 1-2s é uma expansão isentrópica

s 1 = s 2 s → 6,9072 = 0,5926 + x 2 s ⋅ 7,6361

→ x 2 s = 0,8269

A entalpia é dada por

h 2 s = h f + x 2 s ⋅ h f g = 173,88 + 0,8269 ⋅ 2403,1 = 2161,003   k J / k g

Usando a eficiência isentrópica da turbina

η T = h 1 - h 2 h 1 - h 2 s → 0,88 = 2545,3 - h 2 3545,3 - 2161,003

→ h 2 = 2327,118   k J / k g

No estado 3

h 3 = h f = 173,88   k J / k g

Passo 5

Trabalho isentrópico da bomba

w P = - ∫ v d p = - v f p 4 - p 3 = - 1,0084 ⋅ 10 - 3 80 - 0,08 ⋅ 100 = - 8,0591   k J / k g

Aplicando a equação da energia ao processo 3-4s

Q + h 3 = w p + h 4 → 0 + h 3 = w p + h 4 s

→ h 4 s = h 3 - w p = 173,88 - - 8,0591 = 181,939   k J / k g

Usando a eficiência isentrópica

η P = h 4 s - h 3 h 4 - h 3 → 0,82 = 181,939 - 173,88 h 4 - 173,88

→ h 4 = 183,708   k J / k g

Passo 6

a) a potência desenvolvida

W ˙ t o t = Q e n t - Q s a i = m ˙ h 1 - h 4 - h 2 - h 3

→ W ˙ t o t = 7,8 3545,3 - 183,708 - 2327,118 - 173,88

∴ W ˙ t o t = 9425,1612   k W

Passo 7

b) a eficiência térmica

η = W ˙ t o t Q e n t = W ˙ e n t m ˙ h 1 - h 4 = 9425,1612 7,8 3545,3 - 183,708

∴ η = 35,94 %

Passo 8

c) Das tabelas de vapor com t w ,   e n t = 18 ° C

h w , e n t = 75,58   k J / k g

t w , s a i = 36 ° C

h w , s a i = 150,86   k J / k g

Aplicando o balanço de energia no condensador

m ˙ w h w , s a i - h w , e n t = m ˙ s h 2 - h 3 → m ˙ w 150,86 - 75,58 = 7,8 2327,118 - 173,88

∴ m ˙ w = 223,1   k g / s

Resposta

a) W ˙ t o t = 9425,1612   k W

b) η = 35,94 %

c) m ˙ w = 223,1   k g / s

Ver Outros Exercícios desse livro