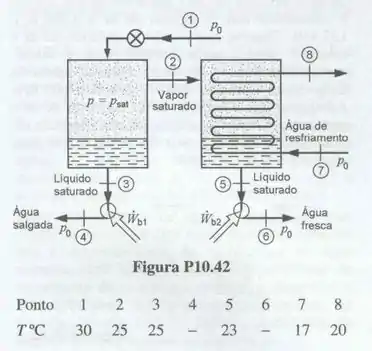
Água potável pode ser produzida a partir da evaporação de água salgada e posterior condensação do vapor gerado. Um esquema deste processo, que utiliza água salgada efluente no condensador de uma usina termoelétrica, está mostrado na Fig. P10.42. A vazão de água salgada no ponto 1 é e no ponto 2 o vapor está no estado saturado. Este vapor é, então, condensado a partir da transferência de calor para a água salgada. Note que é necessário utilizar uma bomba no escoamento de água potável, para aumentar a pressão até , porque a pressão utilizada no evaporador instantâneo (flash) é menor que a atmosférica. Utilizando as variáveis de processo mostradas na figura, admitindo que as propriedades da água salgada sejam as mesmas da água pura, que a temperatura do ambiente seja e que os equipamentos são adiabáticos, determine a taxa de geração de irreversibilidade no processo de estrangulamento da água salgada e no condensador.

Seguindo, devemos aplicar a equação da continuidade no nosso sistema analisando o estrangulador:

Aplicando a equação de energia e entropia, temos:

Com a relação obtida com a equação de energia podemos calcular o título do nosso sistema:

Agora, podemos calcular a entropia de saída:

Assim, jogando na equação de entropia obtemos :

Pela equação da continuidade obtemos a massa de vapor saturado saindo:

A primeira parte do nosso problema nos pede que determinemos a taxa de geração de irreversibilidade no processo de estrangulamento da água salgada:

Partindo para a análise do condensador, aplicando a equação de energia, temos:

Isolando :

Substituindo os dados:

Aplicando a equação de entropia:

Sendo a taxa de geração de irreversibilidade dada por:

Isolando e substituindo na equação de geração de irreversibilidade, temos:

Assim finalizamos o nosso problema.

Até a próxima!