Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 146
Água subterrânea está sendo bombeada para uma piscina com área superficial de 6 m x 9 m, enquanto a água da piscina é despejada por um orifício com 7 cm de diâmetro a uma velocidade
média constante de 4 m/s. Considerando que o nível da água da piscina se eleva a uma taxa de 2,5 cm/min, determine a taxa com a qual a água é fornecida para a piscina, em m³/s.
Passo 1
Entendendo o problema:
Ne problema, água está sendo bombeada para uma piscina e ao mesmo tempo escoando da piscina através de um orifício. A Figura 1 esquematiza o processo. O enunciado informa os dados a respeito da vazão do orifício pelo qual a água deixa a piscina, e também informa a taxa de acúmulo de água. O problema pede então a taxa volumétrica com que a água está sendo fornecida para a piscina.
Figura 1: Água sendo bombeada para uma piscina e ao mesmo tempo vazada através de um orifício
Ao observar o princípio da conservação de massa, a quantidade de água acumulada na piscina é igual a quantidade que é fornecida menos a quantidade que deixa o recipiente pelo orifício. Matematicamente, este balanço de massa é dado por:
(1)
A água para esse caso pode perfeitamente ser admitida como um fluido incompressível, o que significa que sua densidade é constante. Relembrando a relação entre massa, densidade e volume, uma vez que a densidade é constante, a conservação de massa se aplica também ao volume. Assim a equação (1) pode ser escrita para o volume:
(2)
Ou seja, a taxa volumétrica com que a água é fornecida à piscina, 
é igual à variação de volume de água na piscina somada com a taxa volumétrica com que a água sai pelo orifício.
Passo 2
Calculando a taxa volumétrica de saída e a taxa de acúmulo de volume de água na piscina:
Deve-se lembrar que a taxa volumétrica de fluido que atravessa uma determinada área é dada pelo produto de velocidade do fluido pela área de seção transversal. Assim:
(3)
A velocidade com que a água atravessa o orifício, bem como suas dimensões são informadas no enunciado do problema. Substituindo os valores, a taxa volumétrica de saída é
O problema fornece a área superficial da piscina e também a taxa com que a altura da água na piscina aumenta. A taxa de acúmulo do volume de água pode então ser calculada, uma vez que é o produto dessas duas grandezas. Então:
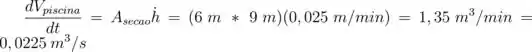
Passo 3
Calculando a taxa volumétrica de entrada:
De posse da taxa volumétrica de saída e da taxa de acúmulo, recorremos à equação (2) para calcular a taxa volumétrica de entrada. Assim:
Resposta
Taxa de água fornecida à piscina: 