Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 6.Problemas - Ex. 24
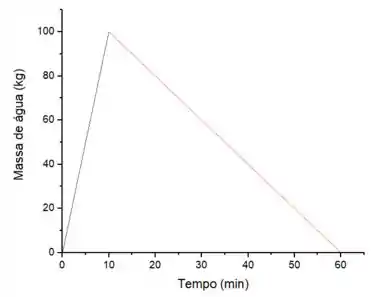
Uma banheira que, inicialmente, estava vazia e com o ralo tampado está sendo alimentada com quilogramas de água por minuto. Após minutos do início da operação de enchimento, a tampa do ralo foi retirada e a vazão de alimentação de água foi reduzida de quilogramas por minuto para quilogramas por minuto. Considere que a vazão em massa de água no ralo é constante e igual a quilogramas por minuto. Faça um gráfico da massa de água contida na banheira em função do tempo. Determine o tempo necessário para que não exista água na banheira. Considere que o intervalo de tempo inicia na partida da primeira operação de enchimento da banheira.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Neste exercício devemos ter bastante atenção às informações do enunciado para não nos perdermos. Vamos por partes!
Em um primeiro momento, a banheira está vazia e com ralo tampado, sendo então alimentada com uma vazão constante de durante .
Ou seja, neste primeiro momento só temos o escoamento de entrada. A banheira está somente enchendo. Se a vazão é de e se passaram , então:
Temos então na banheira um total de de água.
Passo 2
O ralo é então aberto e a vazão de entrada é diminuída para . Temos que a vazão de saída provocada pela abertura do ralo é de .
Bom... Se está entrando menos água do que está saindo, a banheira está secando. A vazão resultante é de:
Se a banheira estava com de água, e temos a vazão resultante, podemos descobrir o tempo necessário para retirar (secar) estes de água. Temos que:
Ou seja, nas condições dadas, demoraria para que a banheira fosse totalmente secada.
O tempo total do processo, seria a soma dos iniciais com os do segundo momento:
Passo 3
Agora que temos todos os dados, podemos construir nosso gráfico do processo para a quantidade de massa de água em função do tempo:
