Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 6.Problemas - Ex. 91
O aquecedor de mistura de uma central térmica é alimentado com de água a e com vapor descarregado de uma turbina a . Admitindo que o aquecedor descarregue a água como liquido saturado, determine a vazão de Vapor proveniente da turbina.
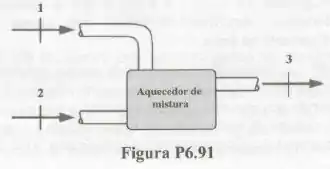
Passo 1
Neste exercício, temos um sistema com duas entradas e uma saída. Queremos a vazão de vapor proveniente da turbina. Analisando a figura do enunciado, vamos chamar este dado de .
Temos a seguinte equação de energia para o nosso exercício:
Pela equação da continuidade, sabemos que:
Portanto:
Resolvendo a nossa equação para , temos:
Passo 2
As entalpias específicas de cada seção podem ser encontradas a partir das tabelas de propriedades termodinâmicas para os fluidos. Temos que:
Logo:
Resposta
Exercícios de Livros Relacionados
16- Os sentidos dos escoamentos num trocador de calor duplo tubo são iguais ( o equipamento opera de modo co-corrente). O tubo interno é alimentado com 1k g / s de ar a 500K e o externo com 2k g / s d
14- Água evapora no interior do tubo de uma caldeira que opera a 100k P a . A velocidade do escoamento de líquido saturado que alimenta o tubo é 1m / s e o tubo descarrega vapor saturado a 100k P a .Q
Um jato d'água a alta velocidade é utilizado como elemento cortante numa máquina. Admita que a velocidade do jato e o diâmetro do jato são iguais a 1000m / se2m m . A temperatura da água na seção de d
O trocador de calor utilizado numa central de água gelada é alimentado com 2,5k g / s de água a 20 ° C e 100k P a e descarrega a água a 5 ° C . Determine a taxa de transferência de calor da água para
A vazão de ar num condicionador é 0,5k g / s . O equipamento é alimentado com ar a 30° Ce101k P a e descarrega o fluido a 10° Ce101k P a . Determine a taxa de transferência de calor que ocorre no esco