Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 116

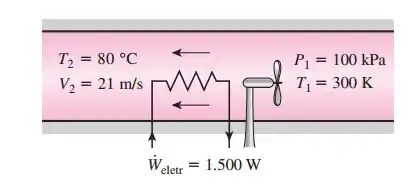
Ar a 300 K e 100 kPa flui em regime permanente em um secador de cabelo que consome 1.500 W. Por causa do tamanho da entrada de ar, a velocidade do ar na entrada é desprezível. A temperatura do ar e a velocidade na saída do secador de cabelo correspondem a 80 °C e 21 m/s respectivamente. O escoamento do ar ocorre a uma pressão constante e de forma adiabática. Considere que o ar possui calores específicos constantes de 300 K. (a) Determine a

vazão mássica de ar no secador de cabelo, em kg/s. (b) Determine a vazão volumétrica de ar na saída do secador de cabelo, em m³/s.

Passo 1

Vamos começar a questão assumindo algumas coisas:

  1. O processo se dá em regime permamente
  2. As variações de energia potencial e cinética são desprezíveis
  3. A perda de calor pelo secador é desprezível

Dados para a questão:

A constante dos gases para o argônio é R = 0,287   K P a . m 3 / k g . K

O calor específico a pressão constante à temperatura ambiente é C p = 1,005   k J / k g ⋅ º C (Tabela A - 2 ) “Calores específicos de gás ideal para diversos gases comuns” da página 909

Passo 2

a)Escrevendo a equação do balanço de energia para o sistema em regime permanente ( Δ E = 0 ) :

E e n t r a d a - E s a í d a = Δ E s i s t e m a E ˙ e n t r a d a   - E ˙ s a í d a = 0 E e n t r a d a = E ˙ s a í d a m ˙ h 1 + V 1 2 2 + W ˙ e n t r a d a = m ˙ h 2 + V 2 2 2 W ˙ e n t r a d a = m ˙ h 2 - h 1 + V 2 2 - V 1 2 2

Usando a relação h = C p T : W ˙ ̇ e n t r a d a = m C p T 2 - T 1 + V 2 2 - V 1 2 2 m ˙ = W ˙ e n t r a d a C p T 2 - T 1 + V 2 2 - V 1 2 2  

Em que T 2 é a temperatura final, T 1 é a temperatura inicial e V 1 e V 2 são as velocidades.

Passo 3

Substituindo T 2 = 80 + 273 = 353 K , W e n t r a d a = 1,5   k W , V 1 = 21   m / s e T 1 = 300   K

m ˙ = 1,5     k W 1,005 k J k g ⋅ K . 353   K - 300 K +   21   m / s 2 - ( 0   m / s ) 2 2 ⋅   1 k J k g 1000 m 2 s 2 m ˙ = 0,0280   k g / s

Portanto, a vazão mássica de ar no secador é 0,0280   k g / s  

Passo 4

b) Escrevendo a equação para o volume específico na saída usando a equação dos gases ideais:

v 2 = R T 2 p 2

Substituindo R = 0,287   k J / k g . K , T 2 = 353   K e P 2 = 100   k P a

v 2 = 0,287 × 353 100 = 1,013   m 3 / k g

Agora podemos utilizar a expressão para calcular a vazão volumétrica:

V ˙ = m ˙ v 2

Substituindo m ˙ = 0,02793   k g / s e v 2 = 1,013   m 3 / k g  

V = 0,02793   k g / s ⋅ 1,013   m 3 / k g = 0,0284   m 3 / s

Portanto a vazão volumérica que sai do secador de cabelo é 0,0284   m 3 / s

Resposta

a ) 0,0280   k g / s b ) 0,0284   m 3 / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Reconsidere o Prob. 5–116. Usando o EES (ou outro programa), investigue o efeito da velocidade de saída sobre a vazão mássica e a vazão volumétrica de saída. Considere que a velocidade de saída varia
Reconsidere o Prob. 5–78. Usando o EES (ou outro programa), investigue o efeito do fluxo de massa da corrente fria de R-134a sobre a temperatura e o título da corrente de saída. Varie a razão entre o
3- Um dispositivo que opera em regime permanente pode apresentar trabalho de fronteira?
4- Como variam as vazões em massa e em volume num dispositivo que opera em regime permanente?
110- Um recipiente rígido, inicialmente em vácuo, é carregado com água, proveniente de uma tubulação, a 0.8M P a e 350° C . Admita que o processo de enchimento é adiabático e que o recipiente é lacrad