Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 5.Problemas - Ex. 30

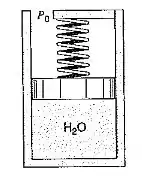
Um arranjo cilindro-pistão tem a pressão atmosférica e uma mola linear agindo sobre o pistão, conforme mostrado na Fig. P5.30. O arranjo contém água a 3   M P a e 400 ° C com um volume de 0,1   m 3 . Se o pistão estiver encostado no fundo do cilindro, a mola toca o pistão, mas não exerce força sobre ele, e a pressão interna necessária para iniciar o movimento do pistão, nesta condição, é de 200   k P a . O sistema é então resfriado até que a pressão atinja 1   M P a . Determine a transferência de calor para esse processo.

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Nós temos os seguintes dados para a água, segundo o enunciado

T 1 = 400 ° C

V 1 = 0,1   m 3

P 1 = 3   M P a

P 0 = 200   k P a

P 2 = 1   M P a

Da tabela de água superaquecida com valores correspondentes a P 1 = 3   M P a e T 1 = 400 ° C , podemos obter o volume específico inicial e a energia interna

v 1 = 0,09936 m 3 k g

u 1 = 2932,75 k J k g

A massa de água é igual a

m = V 1 v 1 = 0,1 0,09936 = 1,0064   k g

A relação entre pressão e volume é linear, então podemos escrever o termo para a pressão final assim:

P 2 = P 1 - P 0 v 1 ∙ v 2 + P 0

Invertendo, podemos calcular o volume específico final

v 2 = P 2 - P 0 P 1 - P 0 ∙ v 1

Substituindo os valores,

v 2 = 1000 - 200 3000 - 200 ∙ 0,09936 = 0,02839 m 3 k g

Passo 2

Da tabela de água saturada B.1.2 com valores correspondentes a P 2 = 1000   k P a , nós podemos obter o volume específico e a energia interna

v f = 0,001127 m 3 k g

v f g = 0,19332 m 3 k g

u f = 761,67 k J k g

u f g = 1821,97 k J k g

O volume específico final é dado por:

v 2 = v f + x ∙ v f g

Isolando o x , podemos calcular o fator de qualidade

x = v 2 - v f v f g = 0,02839 - 0,001127 0,19332 = 0,141

Podemos inseri-lo agora em um termo para energia interna específica final:

u 2 = u f + x ∙ u f g = 761,67 + 0,141 ∙ 1821,97 = 1018,567 k J k g

Passo 3

O trabalho realizado é igual a

W = ∫ P   d V = P m e d ∙ V 2 - V 1

Com isso, nós temos que

W = P 1 + P 2 2 ∙ m ∙ v 2 - v 1

Substituindo os valores

W = 3000 + 1000 2 ∙ 1,0064 ∙ 0,02839 - 0,09936 = - 142   k J

A transferência de calor é dada por

Q = m u 2 - u 1 + W = 1,0064 ∙ 1018,567 - 2932,75 - 142 = - 2056   k J

Portanto,

Q = - 2056   k J

Resposta

Q = - 2056   k J

Exercícios de Livros Relacionados

Um recipiente rígido equipado com um agitador contém 1,5 k g de óleo de motor. Determine a taxa de aumento da energia específica, considerando que o calor é transferido para o óleo a uma taxa de 1 W e
Um sistema fechado passa por um processo em que não há mudança na energia interna. Durante esse processo, o sistema produz 1,1 x 10 6l b f . p é é de trabalho. Calcule a transferência de calor para es
Complete a Tabela seguinte com base no princípio de conservação da energia para um sistema fechado.
Uma determinada quantidade de vapor de água, saturado em um sistema fechado, é condensada até se tornar líquido saturado a 40 k P a . Determine o calor transferido e o trabalho realizado durante esse
Uma certa massa de vapor saturado de R-134a a 100 ° F é condensada a uma pressão constante até se tornar líquido saturado em um sistema fechado pistão-cilindro. Calcule a transferência de calor e o tr