Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 3.Problemas - Ex. 53

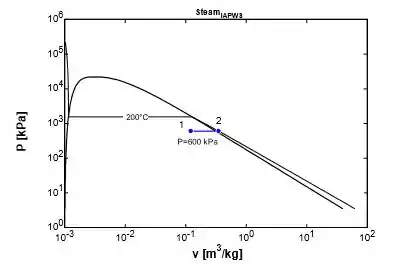
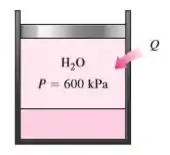
Um arranjo pistão-cilindro contém 0,005de água líquida e 0,9de vapor de água em equilíbrio a 600 kPa. Calor é transferido a pressão constante até que a temperatura atinja 200 °C. a) Qual é a temperatura inicial da água?

b) Determine a massa total da água.

c) Calcule o volume final.

d) Mostre o processo em um diagrama P-v com relação às linhas de saturação.

Passo 1

Na letra a, inicialmente duas fases coexistem em equilíbrio, portanto, temos uma mistura saturada de vapor líquido. Então a temperatura no tanque deve ser a temperatura de saturação na pressão especificada:

Passo 2

Na letra b, a massa total neste caso pode ser facilmente determinada pela adição da massa de cada fase,

Passo 3

Na letra c, no estado final, a água é vapor superaquecido e seu volume específico é (olhar tabela A-6):

Então,

Passo 4

Na letra d, temos o diagrama:

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

a) Mostre que as constantes críticas de uma substância obedecem à equação de Dieterici de estado, P v - be a v R T = R T , são P C = a 4 e 2 b 2 ,v C = 2 b ,T C = a 4 R b b) Compare a razão P C v C /

a) Usando a relação cíclica Eq. (2-41), encontre o coeficiente de dilatação β de uma substância que obedece à equação de Dieterici de estado, dada no problema 2.30.b) A altas temperaturas e grandes vo

Usando as constantes críticas encontradas na T a b e l a2.3 , calcule o valor de b na equação de van der Waals para o C O 2 (a) a partir de v c e (b) a partir de T c e P c .

Determine a fase, o título (se for o caso) e a propriedade que falta, P ou T .a. H 2 OaT = 120 ° C ,c o mv = 0,5m 3 / k g b. H 2 OaP = 100k P a ,c o mv = 1,8m 3 / k g c. H 2 OaT = 263K ,c o mv = 200m