Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 191
Um arranjo pistão-cilindro vertical isolado contém inicialmente de ar a 150 kPa e . Nesse estado, uma mola linear toca o pistão, mas exerce nenhuma força sobre ele. O cilindro está conectado por uma válvula a uma linha que fornece ar a 700 kPa e 22ºC. A válvula é então aberta, e o ar da linha de alta pressão entra no cilindro. A válvula é fechada quando a pressão interna do cilindro atinge . Considerando que o volume interno do cilindro dobra durante esse processo, determine (a) a massa do ar que entrou no cilindro e (b) a temperatura final do ar dentro do cilindro.
Passo 1
Para resolver essa questão vamos precisar de alguns dados da Tabela A-1 e Tabela A-2:
e
E precisamos lembrar as seguintes relações:
Lembre-se também a energia em um fluido estacionário é determinada pela energia interna; e para um fluido em escoamento a energia é determinada pela entalpia.
Passo 2
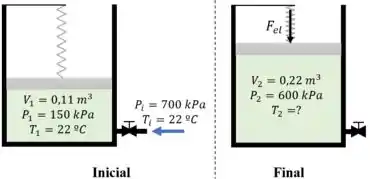
Vamos fazer um balanço de massa. A soma da massa inicial mais a massa que entra é igual a massa final :
Podemos calcular as massas utilizando a equação dos gases ideais:
Então, a equação de massas é:
Passo 3
Já sabemos dos capítulos anteriores que o trabalho realizado pelo deslocamento de um cilindro é:
Vamos considerar que todo o trabalho é absorvido para a mola:
Passo 4
A melhor forma de começar questões desse tipo é fazendo os balanços energia
Vamos expandir o balanço de energia, no instante (1) temos a energia contida no cilindro e a energia que entra pela válvula; no instante (2) temos a energia contida no cilindro e o trabalho que a mola realiza sobre o pistão.
Sabemos que e :
Aplicando os valores dados pela questão e que já calculamos para as massas e para o trabalho:
Passo 5
Pronto! Agora que temos a temperatura, vamos calcular a massa final:
Logo, a variação de massa no sistema é: