Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 193

A bomba de um sistema de distribuição de água é acionada por um motor elétrico de 6kW cuja eficiência é de 95%. A vazão de água na bomba é de 18 L/s. Os diâmetros dos tubos de entrada e saída são iguais, e a diferença de altura ao longo da bomba é desprezível. Considerando os valores das pressões de entrada e saída da bomba 100 kPa e 300 kPa (absoluta) respectivamente, determine (a) a eficiência mecânica da bomba e (b) o aumento da temperatura da água à medida que ela escoa pela bomba devido à ineficiência mecânica.

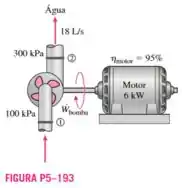
Passo 1

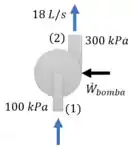
A potência da bomba pode ser calculada utilizando a potência e eficiência do motor:

W ˙ b o m b a = η m o t o r ⋅ W ˙ m o t o r

W ˙ b o m b a = 0,95 ⋅ 6   k W

W ˙ b o m b a = 5,7   k W

Passo 2

Para calcular a energia do fluxo, precisaremos da vazão mássica:

m ˙ = ρ V ˙

m ˙ = 1 k g L ⋅ 18 L s

m ˙ = 18 k g s

Passo 3

Sabemos que:

Q ˙ - W ˙ = m ˙ P ρ + V 2 2 + g z s a i - m ˙ P ρ + V 2 2 + g z e n t r a  

No processo não há transferência de calor, e o trabalho é o fornecido pela bomba. Contudo, nem toda energia que a bomba fornece é de fato absorvida pelo fluxo. Se considerarmos que na entrada e na saída toda energia do fluido está em forma de pressão:

W ˙ a b s o r v i d o = m ˙ ρ P 2 - P 1  

Além disso, não há

W ˙ a b s o r v i d o = 18   k g / s 1000   k g / m 3 300   k P a - 100   k P a  

W ˙ a b s o r v i d o = 3,6   k W  

Passo 4

A eficiência da bomba é igual a potência que o fluxo absorve, divido pela potência que a bomba fornece:

η b o m b a = W ˙ a b s o r v i d o W ˙ b o m b a

η b o m b a = 3,6 5,7

η b o m b a = 63,16 %

Passo 5

Para calcular o aumento de temperatura da água, vamos imaginar que toda a energia perdida será absorvida pela água em forma de calor:

E p e r d i d a = W ˙ b o m b a - W ˙ a b s o r v i d o

E p e r d i d a = 5,7 - 3,6

E p e r d i d a = 2,1   k W

A variação de temperatura pode ser calculada pela fórmula da calorimetria:

Q = E p e r d i d a

m c p Δ T = E p e r d i d a

Δ T = E p e r d i d a m c p

Δ T = 2,1   k W 18 k g s ⋅ 4,18 k J k g ⋅ K

Δ T = 0,028   º C

Resposta

η b o m b a = 63,16 %

Δ T = 0,028   º C

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força motriz para o escoamento de fluidos é a diferença de pressão, e uma bomba opera elevando a pressão de um fluido (convertendo o trabalho mecânico de eixo em energia de escoamento). O consumo de
Um ventilador deve acelerar o ar parado até a velocidade de 12 m/s a uma taxa de 3 m 3 / s . Considerando que a densidade do ar é de 1,15 kg/ m 3 , a potência mínima que deve ser fornecida ao ventilad
Uma bomba de 2 kW é usada para bombear querosene ( ρ = 0,820k g / L ) de um tanque no solo até um tanque em uma posição mais alta. Ambos os tanques são abertos para a atmosfera, e a diferença de altur
Refrigerante 134a entra em um compressor com um fluxo de massa de 5 kg/s e a uma velocidade desprezível. O refrigerante entra no compressor como vapor saturado a 10 °C e deixa o compressor a 1.400 kPa
Um compressor de ar comprime 15 L / s de ar a 120 kPa e 20 °C para 800 kPa e 300 °C enquanto consome 6,2 kW de potência. Quanto dessa potência está sendo utilizada para aumentar a pressão do ar, e qua