Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 5.Problemas - Ex. 190
Considere um aquecedor de água que consiste em um tubo isolado com 5 cm de diâmetro com um resistor elétrico em seu interior: adiciona-se água fria a 20ºC na seção de aquecimento em regime permanente com vazão de 30 L/min. Considerando que a água deve ser aquecida a 55ºC, determine: (a) a potência nominal do aquecedor elétrico e (b) a velocidade média da água no tubo.
Passo 1
Vamos calcular algumas propriedades úteis. Primeiro, o calor específico da água é tabelado:
A questão não nos dá a vazão mássica , mas sim a vazão volumétrica . Para conseguir a vazão mássica basta multiplicar pela densidade:
Passo 2
Observe a situação descrita na questão:
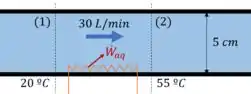
Vamos considerar que não há perdas, e que todo o calor do aquecedor é absorvido pela água. Em outras palavras, toda a potência se transforma em calor que altera a temperatura da água:
Passo 3
Pra calcular a velocidade é bem simples, a vazão volumétrica é igual ao produto entre a área e a velocidade
Como o fluxo está contido em um tubo, a área é igual a área da circunferência:
Isolamos a velocidade:
Vamos converter o diâmetro e a vazão para metros: