Um automóvel com 900 kg de massa inicialmente se move ao longo de uma estrada a 100 km/h em relação a esta. Em seguida, sobe uma colina cujo cume está a 50 m acima do nível da estrada e de parques em uma área de descanso localizada ali. Determine as variações das energias cinética e potencial para o automóvel, ambas em kJ. Para cada quantidade de energia, cinética e potencial, especifique a escolha do ponto de partida e o valor de referência adotada neste. Considere g = 9,81 m/s².
Passo 1
Vamos resolver mais essa galerinha. A questão é representada pelo esquema abaixo. Vamos considerar que o ponto inicial para os nossos cálculos o automóvel tem a velocidade de 100 km/h e está no nível de referência (z = 0). Quando ele chega no cume, vamos considerar que o carro para.
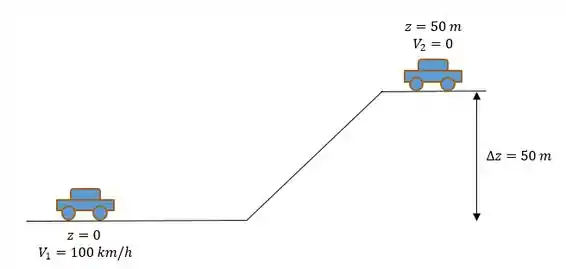
Vamos lembrar primeiro como calcula a variação de energia cinética e de energia potencial:
Passo 2
Vocês podem observar que a velocidade está em km/h. Por isso, na fórmula de energia cinética, tem que dividir a velocidade por 3,6. Assim
Convertendo para kJ
Passo 3
A variação de energia potencial é:
Fazendo a conversão para kJ: