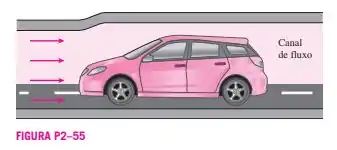
Um automóvel movendo-se através do ar faz com que a velocidade do ar (medida em relação ao carro) diminua e preencha um canal de fluxo maior. Um automóvel tem uma área de canal de fluxo efetivo de 3 . O carro está viajado a 90 km/h em um dia em que a pressão barométrica é de 70 cm de mercúrio e a temperatura é de 20 °C. Atrás do carro, a velocidade do ar (em relação ao carro) é medida em 82 km/h, e a temperatura é de 20 °C. Determine a potência necessária para mover o carro através do ar e a área do canal de fluxo efetivo por trás do carro.

Para descobrirmos o fluxo de ar do processo, utilizaremos a seguinte expressão:

Onde, é a área do canal na frente do carro, a velocidade do ar na frente do carro e o volume específico do ar.

Para calcularmos o volume específico do ar, temos:

Onde, R é a constante dos gases, T a temperatura do ar (em K) e P a pressão.

Vamos converter mm de Hg para kPa, temos que 1 mm de Hg equivalem a 0,133 kPa, assim, 700 mm de Hg equivalem a 93,1 kPa, logo:

Assim, teremos que o fluxo mássico de ar será equivalente a:

Agora, substituindo os dados na nossa expressão de potência, teremos:

Agora, como temos o fluxo mássico, também conseguimos descobrir a área do canal de fluxo de ar atrás do carro, temos que o fluxo mássico é o mesmo na frente e atrás do carro, o que vai mudar é apenas a área, então: