Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 2.Problemas - Ex. 39
Um automóvel quebrado que pesa 1.200 kg está sendo guinchado por um caminhão. Desprezando o atrito, o arrasto aerodinâmico e a resistência ao rolamento, determine a potência extra necessária para manter uma velocidade constante em uma estrada plana, para obter uma velocidade constante de 50 km/h em uma estrada com 30° de aclive (com a horizontal) e para acelerar em uma estrada plana do repouso a 90 km/h em 12 s.
Passo 1
Inicialmente, na alternativa temos que o caminhão guinchando o veículo quer manter uma velocidade constante em uma estrada plana. A única energia mecânica atuando nesse caso é a energia cinética, logo, um trabalho cinético será realizado para isso e, daí, uma potência gerada. A expressão para a potência do trabalho cinético é dada por:
Temos que, como a velocidade é constante, a variação da velocidade será nula, daí, teremos que a potência do trabalho cinético também será nula.
Passo 2
Na alternativa além do trabalho cinético, também teremos um trabalho potencial, pois o caminhão guinchando o veículo estará em uma estrada em aclive, ou seja, existirá uma diferença na altura entre a base da estrada e o topo.
Porém, também teremos que a velocidade está constante, ou seja, a potência do trabalho cinético será nula pela falta da variação da velocidade.
Vamos então calcular a potência do trabalho potencial, mas antes, vamos encontrar a altura em que o caminhão está, para isso, iremos considerar que o caminhão percorreu 1h de percurso, e, com a velocidade que ele está, percorreu 50km.
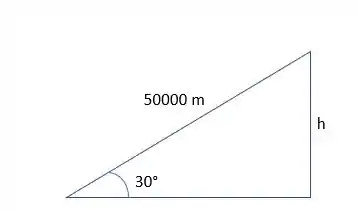
Teremos então que a altura será dada por:
Assim, utilizando a expressão da potência gravitacional, teremos:
Passo 3
Na alternativa temos uma estrada plana, então não teremos a potência do trabalho potencial. Diferente das outras alternativas, aqui o caminhão parte do repouso até atingir uma velocidade final de 90 km/h, ou seja, existe uma diferença, uma variação na velocidade.
Inicialmente, vamos converter a velocidade em km/h para m/s, para isso, basta dividir por 3,6:
Agora, utilizando a expressão da potência do trabalho cinético, teremos:
Resposta
;
;
;