Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 5.Problemas - Ex. 112
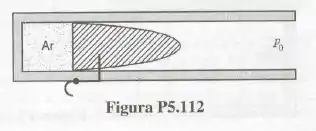
A Fig. P5.112 mostra o esquema de uma pistola a ar comprimido. Admita que, quando a pistola está carregada, o volume do reservatório de ar é , a temperatura do ar é e sua pressão é igual a . A massa do projétil é e ele se comporta como um pistão que, inicialmente, está travado por um pino (gatilho). Quando a arma é disparada o ar expande num processo isotérmico e a pressão do ar, no instante em que o projétil deixa o cano, é igual a . Nestas condições, determine:
a. O volume final e a massa de ar contida na pistola.
b. O trabalho realizado pelo ar contido na pistola e o trabalho realizado na atmosfera.
c. O trabalho realizado no projétil e sua velocidade na seção de saída do cano.
Passo 1
Ooi galerinha, tudo bom? Bora resolver essa aqui comigo?
Galera temos um processo de expansão e temos que determinar vários itens, ao decorrer do exercício vamos abordando como resolver cada item.
Ao ler o enunciado ela assusta né, mas fica tranquilo temos uma dica muito boa. Quando o enunciado fala “o ar expande num processo isotérmico” isso significa para nós que o processo é isotrópico com , logo:
Saber o coeficiente isotrópico é tão relevante que devido a ele ser a fórmula do trabalho realizado pelo ar é:
Bora determinar os itens do enunciado.
Passo 2
a) Para letra a temos que calcular o volume final e a massa contida na pistola.
Vamos começar com a massa.
Gente do momento inicial até o final, temos que nenhuma massa de ar escapa do cano da arma, logo, como todo processo de conjunto cilindro – pistão.
E para o cálculo da massa vamos assumir que o ar é um gás ideal, aplicando a fórmula do gás ideal:
Como temos todas as variáveis do estado inicial iremos utilizar elas e olhando na tabela temos que .
Antes de substituir os valores temos que converter a unidade do volume e da temperatura:
Substituindo valores:
Passo 3
a)Para calcular o volume final pessoal temos que utilizar as relações de de processos isotrópicos, a que iremos usar é a seguinte:
Isolando :
Substituindo valores:
Letra a finalizada bora para b.
Passo 4
b) No item b temos que determinar o trabalho realizado pelo ar e o trabalho realizado pela atmosfera.
Pessoal o trabalho par o ar é determinar pela fórmula dita no passo 1, reescrevendo ela:
Substituindo valores:
Passo 5
b) Para o cálculo do trabalho realizado pela atmosfera.
Pessoal à pressão que atmosfera realiza do início ao final do processo é a mesma, logo, .
Como a pressão é constante podemos utilizar a definição de trabalho, que é a seguinte:
Calculando o trabalho:
Olhando no final do livro na página , temos .
Substituindo valores:
Passo 6
c)Para o letra c temos que determinar o trabalho realizado pelo projétil e a velocidade de saída da bala.
Galera o trabalho realizado pela bala nada mais é que o somatório de trabalho aplicado a ela, ou seja, temos o trabalho do ar é acrescenta energia cinética na bala e temos o trabalho da atmosfera retirar energia cinética do projétil.
Escrevendo matematicamente, temos:
Já emendando o outro item a velocidade de saída do projétil, lembra que falei de energia cinética, então haha, a fórmula de energia cinética é definida por:
Como enérgica cinética e trabalho possuem mesma unidade, estamos falando da mesmo item, a energia que faz a bala se mover é o trabalho da bala.
Isolando a velocidade, temos:
Convertendo a massa de gramas para , e substituindo valores:
É isso pessoal, te vejo na próxima.
Resposta
a)
b)
c)