Ar a 2 bar e 380 K é extraído do compressor principal de um motor de avião a jato para o resfriamento da cabina. O ar extraído entra em um trocador de calor, onde é resfriado a pressão constante até 320 K por transferência de calor para o ambiente. Em seguida, expande-se adiabaticamente em uma turbina até 0,95 bar e é descarregado na cabina. A turbina tem uma eficiência isentrópica de 75%. Se a vazão mássica do ar for de 1,0 kg/s, determine
(a) a potência desenvolvida pela turbina, em kW.
(b) a taxa de transferência de calor do ar para o ambiente, em kW.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
É dado que:
- Temperatura de extração do ar:
- Pressão de extração do ar:
- Temperatura na saída do trocador de calor:
- Pressão na saída da turbina:
- Taxa de vazão mássica:
- Eficiência isentrópica da turbina:
O diagrama é mostrado abaixo
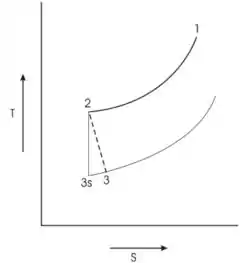
Passo 3
Vamos buscar os dados necessários pra fazer os cálculos primeiro, beleza?
Da tabela de propriedades do ar como gás ideal a
Da tabela de propriedades do ar como gás ideal a
Passo 4
Usando a relação isentrópica para o processo 2-3s
Da tabela de propriedades do ar como gás ideal a , interpolando
Passo 5
Usando a eficiência isentrópica da turbina
Passo 6
Agora que conseguimos os dados, vamos calcular o que a questão pede
a) a potência desenvolvida pela turbina
Passo 7
b) a taxa de transferência de calor do ar para o ambiente é
Já que a pressão permanece constante, o trabalho é igual a zero ()
O sinal negativa significa que o calor é perdido pelo sistema
Resposta
a)
b)