Uma bomba de calor por compressão de vapor com uma capacidade de aquecimento de 500 kJ/min usa Refrigerante 134a como fluido de trabalho. A eficiência isentrópica do compressor é 80%. A bomba é acionada por um ciclo de potência com uma eficiência térmica de 25%. No ciclo de potência, 80% do calor rejeitado são transferidos para o espaço aquecido. Os estados principais estão numerados conforme a Fig. 10.3.
(a) Determine a potência de acionamento do compressor da bomba de calor, em kW.
(b) Calcule a razão entre a taxa de calor total que é enviada para o espaço aquecido e a taxa de calor fornecida ao ciclo de potência. Discuta o resultado.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
Pegando as propriedades de R134a a da “Propriedades de R134a Saturado: Tabela de Temperatura”, usando interpolação
Passo 3
Desenhando o diagrama da bomba de calor
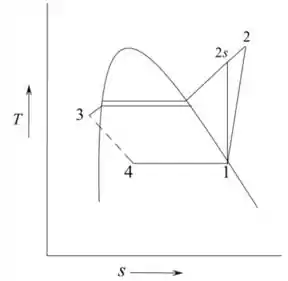
Passo 4
O processo 1-2s é uma compressão isentrópica, então a entropia permanece constante
Pegando a entalpia no estado 2 a e da Tabela “R134a Superaquecido”
Calculando a entalpia atual no estado 2 usando eficiência isentrópica do compressor
Passo 5
O estado está na região de líquido comprimido já que a pressão de saturação () é maior que a pressão no estado 3,
Então, pegamos as propriedades no estado 3 é aproximadamente igual as propriedades de líquido saturado em
O processo 3-2 é uma expansão estrangulada, então
Passo 6
a) Calculando a taxa de vazão mássica do refrigerante usando a capacidade de calor da bomba de calor
Calculando a potência de entrada do compressor
Passo 7
b) calculando o calor de entrada no ciclo de potência
Passo 8
Calculando a quantidade de calor rejeitado
Mas do calor rejeitado é transferido para o espaço.
Passo 9
Calculando a razão da taxa total de calor estragado
Resposta
a)
b)