Uma barra cilíndrica de cobre de área de base e comprimento é isolada ao longo de sua superfície lateral. Uma das extremidades da barra está em contato com uma parede à temperatura . A outra extremidade está em contato com uma parede a uma temperatura baixa . Em regime permanente, a taxa pela qual a energia é conduzida para o interior da barra a partir da parede quente é
Em que é a condutividade térmica da barra de cobre.
a) Considerando a barra como o sistema, obtenha uma expressão para a taxa temporal de geração de entropia em termos de .
b) Se , , e , represente graficamente a taxa de geração de entropia, em , ambos em função de , que varia entre e . Discuta os resultados.
Passo 1
Letra a)
Começamos o nosso problema analisando que o nosso sistema, em estado estacionário, a taxa na qual a energia é conduzida para a haste da parede quente é dada por:
Considerando a haste como um sistema, a taxa de produção de entropia é expressa como:
Aqui, a taxa de variação de entropia é zero.
Assim, o equilíbrio de entropia dá .
Desse modo, a geração de entropia é expressa como:
Substituindo :
Passo 2
Letra b)
Dados:
Substituindo os dados na equação de :
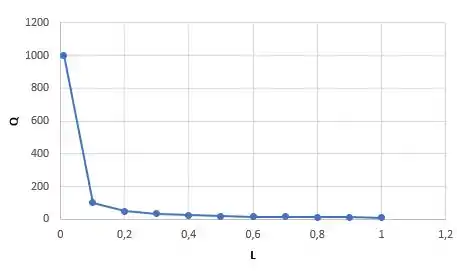
Agora, adotando :

Plotando o gráfico:
Passo 3
Substituindo os dados na equação de :
Agora, adotando :

Plotando o gráfico:
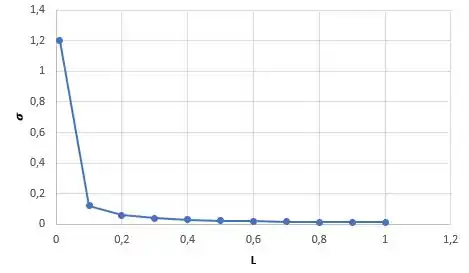
Analisando os gráficos, percebemos que a transferência de calor e a taxa de geração de entropia diminuem com o aumento de .
Até a próxima questão!