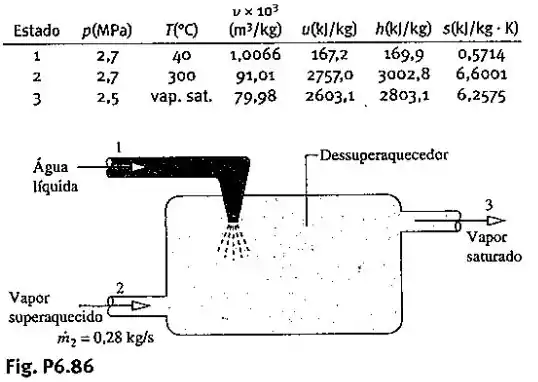
Conforme o dessuperaquecedor ilustrado na Fig. P6.86, água líquida é injetada em um fluxo de vapor superaquecido. Como resultado, tem-se um fluxo de vapor saturado na saída. Os dados para a operação em regime permanente estão apresentados na tabela a seguir. Considere que as perdas de calor e todos os efeitos das energias cinética e potencial são desprezíveis.
a) Localize os estados 1,2 e 3 em um esboço do diagrama .
b) Determine a taxa de geração de entropia no interior do dessuperaquecedor, em .
Passo 1

Fala galerinha!
Bora resolver essa questão juntos?
Se ajeite aí e fica de olho!
Letra a)
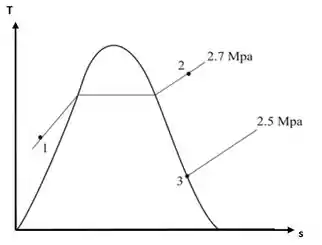
Começamos o nosso problema localizando os estados 1,2 e 3 em um esboço do diagrama :
Passo 2
Letra b)
Agora, devemos aplicar um balanço de energia em nosso sistema:
Como não possuímos transferências de calor e trabalho, além dos efeitos das energias cinética e potencial serem desprezíveis, temos:
Aplicando um balanço de massa:
Substituindo :
Substituindo os dados:
Passo 3
Agora, aplicando um balanço de energia:
Como não temos transferência de calor:
Abrindo a variação de entropia:
Substituindo :
Substituindo os dados:
E assim a gente finaliza a nossa questão!
Até a próxima!