Repita os cálculos do Problema 10.37, considerando Refrigerante 22 como fluido de trabalho. Compare os resultados com os do Problema 10.37 e discuta.
Passo 1
Saalve, tranquilo?
Vamos resolver juntos mais uma questão de termodinâmica?!
Passo 2
Desenhando o diagrama
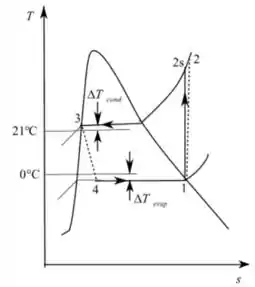
Passo 3
- A taxa de transferência de calor do escritório:
- Queda de temperatura no evaporador:
Passo 4
Da tabela de “Propriedades do Refrigerante 22 Saturado: Tabela de Temperatura” a e vapor saturado
Passo 5
Vamos assumir que a pressão de operação do condensador correspondente a temperatura do condensador
A entropia permanece constante entre os processos 1 e 2s
Agora, da tabela “Propriedades de Refrigerante 22 Superaquecido: Tabela de Temperatura” e e
Conseguimos achar a entalpia no estado 2 usando a interpolação
Mas o compressor opera adiabaticamente com eficiência isentrópica de . Então, a entalpia atual no estado 2 é determinada da relação
Passo 6
O refrigerante deixando o condensador como líquido saturado, então a entalpia no estado 3 é determinada da tabela “Propriedades de Refrigerante 134a Superaquecido: Tabela de Temperatura” a e líquido saturado
O processo 3-4 é estrangulado, então
Passo 7
a) a taxa de vazão mássica do refrigerante é determinada aplicando o palanço de energia para o processo 2 a 3
Passo 8
b) calculando a potência de entrada do compressor
Passo 9
c) calculando o coeficiente de performance do ciclo
Passo 10
calculando o coeficiente de performance da bomba de calor de Carnot
Então, o coeficiente de performance do ciclo de Carnot é maior que o ciclo de Carnot do ciclo original.
Resposta
a)
b)
c) e