Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 151

Calcule a destruição da exergia para cada processo do ciclo Stirling do Prob. 9–81, em kJ/kg.

Passo 1

Do Prob. 9-81, q e n t = 1275   k J / k g ,   q s a í d a = 212.5   k J / k g ,   T 1 = T 2 = 1788   K ,   T 3 = T 4 = 298 K .

A destruição da exergia durante um processo do ciclo é:

x d e s t = T 0 s g e n = T 0 ( Δ s - q e n t T f o n t e + q s a í d a T s u m i d o u r o )

Agora, vamos observar a figura:

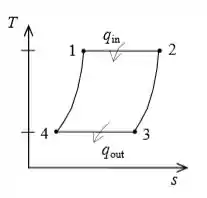
Aplicando essa equação para cada parte do processo:

s 2 - s 1 = c v l n T 2 T 1 + R l n v 2 v 1 = 0.7132   k J / k g . K

x d e s t ,   1 - 2 = T 0 ( s 2 - s 1 - q e n t T f o n t e ) = 0.034   k J / k g ≈ 0

s 4 - s 3 = c v l n T 4 T 3 + R l n v 4 v 3 =   - 0.7132   k J / k g . K

x d e s t ,   3 - 4 = T 0 ( s 4 - s 3 + q s a í d a T s u m i d o u r o ) = - 0.034   k J / k g   ≈ 0

Passo 2

Esses resultados não são surpreendentes, pois o ciclo de Stirling é totalmente reversível. As destruições de exergia não são calculadas para os processos 2-3 e 4-1, porque não há interação com o ambiente durante esses processos para alterar a destruição de exergia.

Resposta

x d e s t ,   1 - 2 = 0.034   k J / k g ≈ 0

x d e s t ,   3 - 4 = - 0.034   k J / k g   ≈ 0

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Um ciclo padrão a ar com calores específicos variáveis executado em um sistema fechado e composto pelos quatro processos seguintes:1-2 Compressão isentrópica de 100 kPa e 22 °C ate 600 kPa2-3 Fornecim
Um ciclo padrão a ar, executado dentro de um sistema pistão-cilindro fechado, e formado por três processos, descritos a seguir:1-2 Fornecimento de calor a V=constante de 100 kPa e 27 °C até 700 kPa2-3
Um ciclo padrão a ar com calores específicos constantes, executado em um sistema pistão-cilindro fechado, e composto dos três seguintes processos:1-2 Compressão isentrópica com uma razão de compressão
Repita o Prob. 9–19E considerando calores específicos constantes a temperatura ambiente.
Um ciclo de Carnot opera entre os limites de temperatura de 300K e 2.000K e produz 600k W de potência útil. A taxa de variação da entropia do fluido de trabalho durante o processo de fornecimento de c