Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 6.Problemas - Ex. 67

Uma câmara de mistura recebe 2   k g / s de R - 134 a a 1   M P a e 100   ° C de uma linha com baixa velocidade. Em uma segunda linha, escoa 1   k g / s de R - 134 a como líquido saturado a 60   ° C , que entra na câmara de mistura a 1   M P a , após passar por uma válvula de expansão. Calor é transferido de forma que o escoamento de saída é vapor saturado a 1   M P a e a 20   m / s . Determine a taxa de transferência de calor e o diâmetro do tubo de saída.

Passo 1

Fala galeraaa!

Vamos começar com a parte conceitual...

O primeiro passo é fazer o esboço para o nosso volume de controle...

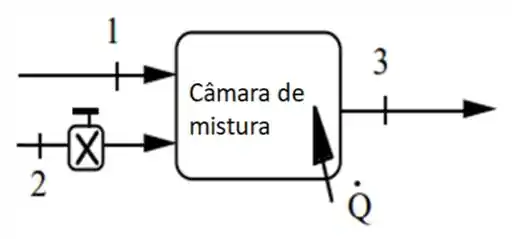
E como sabemos, num volume de controle temos a seguinte fórmula para a conservação de massa...

m ˙ 1 = m ˙ 2 + m ˙ 3

E de acordo com a primeira lei para volumes de controle, temos a seguinte equação de energia...

m ˙ 1 h 1 + m ˙ 2 h 2 + Q = m ˙ 3 h 3 + 1 2 V 3 2

Passo 2

Pois muito bem! O mais importante já temos!

Para o estado inicial... Nas condições 1 e 2... Das tabelas B 5.1   e B 5.2

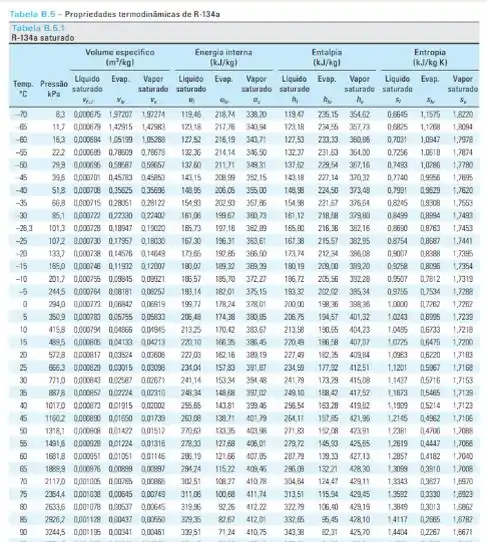
Temos os seguintes valores de entalpia...

E s t a d o   1 → 1   M P a , 100   ° C   ∴ h 1 = 483,36   k J / k g

E s t a d o   2 → x = ∅ , 60   ° C   ∴ h 2 = 287,79   k J / k g

E também podemos obter os valores de entalpia correspondentes ao estado final em ( 3 ) ...

E s t a d o   3 → x = 1 ,   1   M P a ,   V 3 = 20   m / s   ∴ { h 3 = 419,54   k J / k g   v 3 = 0,02038   k J / k g  

Passo 3

Assim, dada a fórmula da conservação de massa do Passo 1, podemos obter a massa em m ˙ 3 :

m ˙ 3 = 1   k g / s + 2   k g / s

m ˙ 3 = 3   k g / s

E com isso, calcular a taxa de transferência de calor...

m ˙ 1 h 1 + m ˙ 2 h 2 + Q = m ˙ 3 h 3 + 1 2 V 3 2

1 ⋅ 287,79 + 2 ⋅ 483,36 + Q = 3 ⋅ 419,54 + 1 2 ⋅ 20 2 ⋅ 1 1000

Q = 4,71   k W

Quanto ao diâmetro do tubo de saída, usando a fórmula abaixo...

A e V 3 = m ˙ 3 v 3

A e = m ˙ 3 v 3 V 3

A e = 3 ⋅ 0,02038 20

A e = 0,003057   m ²

D e = 4 π A e 1 2

D e = 4 π ⋅ 0,003057 1 2

D e = 0,062   m

Resposta

D e = 0,062   m

Exercícios de Livros Relacionados

Um dispositivo que opera em regime permanente é alimentado com 4k g / s de amônia a 150k P ae- 20° C . A amônia é descarregada do dispositivo a 400k P ae80° C . As variações de energia cinética e pote
Um condensador é alimentado com 0,05k g / s de R - 22a800k P ae40° C e descarrega o fluido refrigerante como líquido saturado 15° C . Determine a taxa de transferência de calor neste condensador.
A Fig. P.6.63 mostra o esquema de um aquecedor de C O 2 , que opera em regime permanente. O estado na seção de entrada do aquecedor é T=15 ° Cep=300k P a e o estado na seção de saída é T=1200° Cep =27
A Fig. P6.84 mostra o esboço de um condensador não misturado (trocador de calor) que é alimentado com 1k g / s de água a 300° C e 10k P a e descarrega liquido saturado a 10k P a . O fluido de resfriam
a) Partindo da Equação 6.59, mostre que o coeficiente de acoplamento também pode ser expresso comob) Com base nas frações 21/1 e 12/ 2, explique por que k é menor do que 1,0.