Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 77
Um ciclo Ericsson opera entre reservatórios de energia térmica a produzindo de potência. Determine a taxa de fornecimento de calor para esse ciclo, considerando que ele é repetido vezes por minuto.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Se você não está familiarizado com o ciclo Ericsson, observe abaixo o seu diagrama .
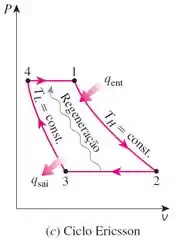
Nos é dito que o ciclo opera entre reservatórios de energia térmica a produzindo de potência. Portanto:
Passo 2
A eficiência de um ciclo ideal é dada por:
Analogamente podemos dizer que:
Da definição, temos também que:
Para um ciclo reversível ideal, temos que:
Logo:
Passo 3
Portanto, temos que:
Logo:
Essa é a taxa total fornecida pelos ciclos por minuto. A taxa por ciclo será então:
Convertendo os ciclos por minuto para ciclos por segundo, temos que:
Logo:
Resolvendo, temos que: