Um ciclo de Rankine ideal com reaquecimento, que utiliza água como fluido de trabalho, opera na entrada da turbina de alta pressão a 8.000 kPa e 450 °C; na entrada da turbina de baixa pressão, a 500 kPa e 500 °C; e no condensador, a 10 kPa. Determine a vazão mássica necessária através da caldeira para que esse sistema produza uma potência líquida de 5.000 kW, e defina a eficiência térmica do ciclo.
Passo 1
Oi pessoal, tudo bem?
Consideremos o esboço para este problema:
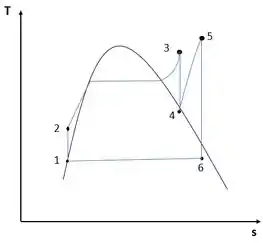
Bem, para início de análise, o problema indica que o estado 1 encontra-se em líquido saturado. Sabemos que o estado 1 encontra-se à mesma pressão do estado 6. Então, utilizando o auxílio das tabelas A.4, A.5 e A6, é possível encontrar algumas relações termodinâmicas.
Passo 2
Temos a pressão de , na tabela de líquido saturado, podemos obter:
Sabendo que o trabalho específico pode ser dado por :
Passo 3
O estado 3 está em vapor superaquecido com e , então:
Sabemos que e que encontra no estado de mistura, portanto há título:
Para encontrar o :
Para o estado 5, sabemos que e e se encontra em vapor superaquecido, das tabelas termodinâmicas: .
Para o estado 6, sabemos que a pressão é de e , então:
Para encontrar o :
Passo 4
Então, o calor que entra é:
Assim, a eficiência térmica é:
𝜂=𝑤𝑞𝑒𝑛𝑡=1548,53921,5
Passo 5
A vazão mássica é dada por:
Resposta
Portanto: e