Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 10.Problemas - Ex. 48

O aquecedor de água de alimentação de um ciclo de Rankine regenerativo fechado deve aquecer água de alimentação a uma pressão de 7000 kPa, inicialmente a 260 °C, até o estado de líquido saturado. As turbinas fornecem vapor extraído a 6000 kPa e 325 °C a essa unidade. Esse vapor é condensado para líquido saturado antes de entrar na bomba. Calcule a quantidade de vapor extraído necessário para aquecer 1 kg de água de alimentação nessa unidade.

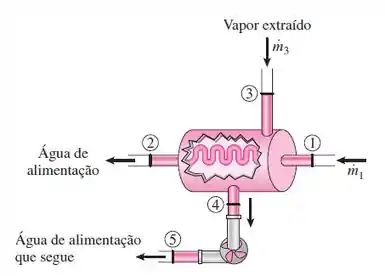
Passo 1

Tá legal! O que vamos fazer primeiro é pegar os dados referentes às entalpias nos pontos de interesse. Dessa forma, consultando as tabelas termodinâmicas e interpolando para obter os valores necessários, temos (iremos denotar o ponto da água de alimentação final, como sendo o ponto 6, que será a junção dos canais 2 e 5):

T 1 = 260   ° C ; p 1 = 7000   k P a   ( á g u a ) → h 1 = 1134,8   k J / k g

T 3 = 325   ° C ; p 3 = 6000   k P a → h 3 = 2964,75   k J / k g

p 6 = 7000   k P a ; x 6 = 0 → h 6 = 1267,5   k J / k g

Passo 2

Então agora podemos calcular o trabalho específico da bomba, que será dado por:

w b = v P 5 - P 4

Então, consultando na tabela termodinâmica na condição 4 a 6000 kPa, teremos o seguinte volume específico:

v = 0,001319   m 3 / k g

Agora, substituindo os valores conhecidos na equação do trabalho da bomba, temos:

w b = 0,001319 7000 - 6000 → w b = 1,319   k J / k g

Agora vamos aplicar o balanço de massa para o sistema, temos:

m ˙ 1 + m ˙ 3 = m ˙ 2 + m ˙ 4

No entanto, sabemos que a água de alimentação, ponto 6, é composta das vazões mássicas 2 e 4, então a equação acima se torna:

m ˙ 1 + m ˙ 3 = m ˙ 6

Passo 3

Agora aplicando o balanço de energia para o sistema:

E ˙ e - E ˙ s = Δ E ˙

Como temos regime permanente, então a energia que entra é igual a energia que sai, então:

E ˙ e = E ˙ s

Sabendo que não temos calor entrando ou saindo do sistema e que podemos desprezar as variações de energia cinética e potencial, dessa forma a equação do balanço de energia se torna:

m ˙ 1 h 1 + m ˙ 3 h 3 + m ˙ 3 w b = m ˙ 6 h 6

Substituindo a relação encontrada para m ˙ 6 , temos:

m ˙ 1 h 1 + m ˙ 3 h 3 + m ˙ 3 w b = m ˙ 1 + m ˙ 3 h 6

m ˙ 1 h 1 + m ˙ 3 h 3 + m ˙ 3 w b - m ˙ 3 h 6 = m ˙ 1 h 6

Isolando m ˙ 3 , temos:

m ˙ 3 = m ˙ 1 h 6 - h 1 h 3 + w b - h 6

Substituindo os valores conhecidos, chegamos em:

m ˙ 3 = 1 1267,5 - 1134,8 2964,75 + 1,319 - 1267,5 → m ˙ 3 = 0,078   k g / s

Resposta

m ˙ 3 = 0,078   k g / s

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A pressão máxima num ciclo de potência a vapor d'água é 5M P a . A temperatura no condensa dor do ciclo é 45° C e a caldeira descarrega o vapor a 600° C . O calor é transferido para a água na caldeira
Um ciclo de potência a vapor d'água, que gera 9,0M W , apresenta pressão máxima igual a 3M P a . A temperatura na seção de descarga da caldeira é 400° C e a pressão no condensador é igual a 50k P a .
A turbina de um ciclo de potência é alimentada com vapor d’água a 5M P a e 400° C . A pressão na seção de descarga da turbina é 10k P a . A eficiência isoentrópica desta turbina é igual a 85 % e a pot
Uma central de potência supercrítica a vapor d'água apresenta pressão máxima de 30M P a e temperatura na seção de saída do condensador igual a 50° C . A temperatura máxima na caldeira é 1000° C , a tu
A Fig. P11.64 mostra uma instalação de cogeração que produz 10k g / s de vapor saturado a 0,5M P a . A instalação é alimentada com água a 20° C e 0,1M P a , a bomba aumenta a pressão no fluido até 5M