Enunciado
Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 11.Problemas - Ex. 78
Em um ciclo de refrigeração, usando R-12 como fluido de trabalho, a vazão de refrigerante é . Vapor de R-12 entra no compressor a e e sai a e . A potência elétrica medida no compressor não adiabático é de . O refrigerante entra na válvula de expansão a e e sai do evaporador a e . Determine a geração de entropia no processo de compressão, a capacidade de refrigeração e o coeficiente de performance para esse ciclo.
Passo 1
Fala, galera! Vamos resolver essa questão.
Vamos começar dando uma olhadinha no diagrama do ciclo para analisar a questão:
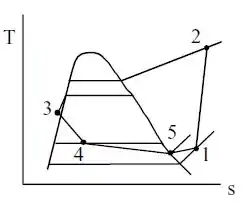
Analisando os estados do diagrama e consultando a tabela B.3, temos:
Estado 1:
Estado 2:
Estado 3:
Estado 5:
Agora vamos às equações!
Passo 2
Na parte do compressor, vamos obter o trabalho específico:
Agora vamos obter o valor da transferência de calor do compressor:
Com esse valor podemos calcular a taxa de geração de entropia pela equação:
Feito isso, agora vamos calcular a taxa de transferência de calor no evaporador com a equação:
Com isso utilizaremos a equação de taxa de transferência de calor para determinar a capacidade de refrigeração:
E finalmente, podemos determinar o coeficiente de desempenho do ciclo:
Prontinho! Até a próxima, galera!