Enunciado
Termodinâmica - Van Wylen- Ed: 6º - Capítulo 11.Problemas - Ex. 119
Um ciclo de refrigeração, que utiliza como fluido de trabalho, opera numa condição onde a temperatura mínima é e pressão máxima é . Admita que o ciclo seja ideal como o da Fig.9.32. Determine as transferências de calor específicas no condensador e no evaporador. Calcule, também, o coeficiente de eficácia do ciclo.
Passo 1
OI OI FALA GALERA! Como vocês estão? Espero que bem! Se liga aí galera que esse problema é sobre ciclo de refrigeração ideal, podemos utilizar a Tabela para encontrar os valores da entalpia que utilizaremos para o calculo das transferências de calor no condensador e no evaporador, logo depois, usaremos o valor dessas transferências para calcular o coeficiente de eficácia do ciclo; E atenção galera, se você não sabe nada sobre ciclo de refrigeração, recomendo da uma olha no conteúdo que o responde aí tem disponível, DEPOIS TU VOLTA MANO! Enfim, dito tudo isto, simbora pra questão!
Passo 2
Primeiramente, observe a imagem abaixo que representa o ciclo de refrigeração ideal com Temperatura inicial de e pressão máxima de :
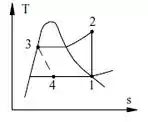
Ok! Observado a figura iremos calcular os valores de entalpia em cada um dos pontos!
No ponto 1, temos uma temperatura de , logo a entalpia e a entropia do vapor saturado no ponto 1 equivale à e . Na saída do condensador (ou seja, no ponto de pressão máxima, que seria o ponto 3) temos uma pressão de , logo, a entalpia de liquido saturado no ponto 3 equivale à . Através da figura sabemos que , logo, através da tabela sabemos que a entalpia no ponto 2 equivale à . (Lembrando que )
Agora com esses dados estabelecidos, podemos calcular o que se pede.
Passo 3
Primeiramente iremos calcular a transferência de calor no evaporador:
Agora iremos calcular a transferência de calor no condensador:
Com isso, calcularemos o coeficiente de eficácia do ciclo:
AÍ ESTÁ, tudo feito com sucesso! É TUDO POR HOJE, bons estudos ;)