Determine quais componentes do ciclo combinado no Prob. 10-85 têm o maior desperdício de potencial de trabalho.
Passo 1
Tá legal, vamos primeiro ilustrar o diagrama T-s do ciclo gás-vapor juntamente com seu diagrama de componentes, lembrando que nesse caso temos eficiência isentrópica a ser aplicada aos dispositivos, então, teremos:

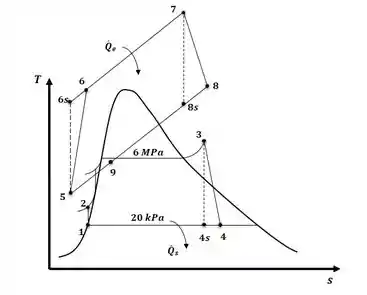
Agora, o que nós vamos fazer agora é trabalhar com o ciclo a gás e algumas relações isentrópicas para descobrir o valor das propriedades nos pontos de interesse. Então, da relação para a temperatura, temos:
Substituindo os valores conhecidos, temos:
Agora, nós sabemos que a eficiência isentrópica do compressor do ciclo superior pode ser dada por:
Escrevendo em função do calor específico, temos:
Substituindo os valores conhecidos, podemos encontrar a temperatura real do ponto 6, então:
Passo 2
Agora, vamos fazer exatamente a mesma análise, só que envolvendo os pontos 7 e 8, entrada e saída da turbina. Então, da relação isentrópica, temos:
Substituindo os valores conhecidos, temos:
Agora, nós sabemos que a eficiência isentrópica da turbina do ciclo superior pode ser dada por:
Escrevendo em função do calor específico, temos:
Substituindo os valores conhecidos, podemos encontrar a temperatura real do ponto 6, então:
E, por fim, para fechar a análise dos pontos do ciclo superior, sabemos que no ponto 9 teremos:
Passo 3
Agora nós vamos encontrar as propriedades do ciclo Rankine inferior com o auxílio das tabelas do apêndice A, então temos:
Com esse volume específico, podemos encontrar o trabalho específico da bomba 1 e depois, a entalpia no ponto 2, então, temos:
E, com isso, aplicando um equilíbrio de energia específica para a bomba 1, temos:
Agora, continuando com o ponto 3, temos:
Então, considerando o processo 3-4 isentrópico, temos:
E, agora, usando a definição de eficiência isentrópica da turbina, temos:
Substituindo os valores conhecidos, conseguimos encontrar a entalpia real do ponto 4:
Então, agora conseguimos encontrar o trabalho líquido específico produzido por cada ciclo, então, para o ciclo a gás, temos:
E, escrevendo em função do calor específico, temos:
E, substituindo os valores conhecidos, chegamos em:
E, para o ciclo Rankine temos:
Substituindo os valores conhecidos, temos:
Passo 4
Agora podemos aplicar um balanço de energia para o trocador de calor do sistema ilustrado no passo 1, dessa forma, teremos:
Como no nosso caso temos regime permanente, então , dessa forma, a equação se torna:
E, colocando em função das entalpias e das vazões mássicas, temos:
Então, agrupando os termos e isolando a massa de vapor, temos:
Escrevendo em função do calor específico do ar e substituindo os valores conhecidos, temos:
Então, 1 kg de gás de exaustão consegue aquecer 0,101 kg de água, dessa forma, podemos encontrar a vazão mássica de ar através da potência líquida dada no enunciado, então, temos:
Então, precisamos calcular o trabalho específico líquido total, que será dado por:
Substituindo os valores conhecidos, temos:
Então, a vazão mássica de gás será:
E, com isso, substituindo esse valor na equação para a vazão mássica de vapor, temos:
Passo 5
Tá legal, agora, para calcular a exergia destruída, e avaliar qual componente têm o maior desperdício de potencial de trabalho, vamos considerar a temperatura da fonte como sendo a temperatura na entrada da turbina do ciclo a gás e a temperatura do sumidouro como sendo a temperatura na saída do condensador, então, temos:
Então, agora vamos calcular os calores que entram e saem do sistema, então, começando pelo processo 2-3, temos:
Para o processo 6-7, temos:
E, o calor que sai do sistema no condensador é dado por:
Para o trocador de calor do problema, sabemos que a exergia destruída pode ser calculada por:
Substituindo os valores conhecidos, chegamos em:
Passo 6
Agora, para o processo 5-6, temos:
Substituindo os valores conhecidos, temos:
Da mesma forma, para o processo 7-8 na turbina a gás, temos:
Substituindo os valores conhecidos, temos:
E, por fim, para o processo 6-7 na câmara de combustão, temos:
Substituindo os valores conhecidos, temos:
Então, como era de se esperar, o maior desperdício de potencial de trabalho acontece durante a adição de calor na câmara de combustão.