Um cilindro de de altura e área da seção transversal de , possui um pistão com massa desprezível, conforme mostrado na Fig. P5.70. Sobre o pistão existe água a e, sob ele, ar a com um volume de . O ar é aquecido causando o movimento para cima do pistão e o transbordo da água para fora do cilindro. Determine a transferência de calor total para o ar quando toda água tiver sido despejada para fora do cilindro.

Vamos começar calculando a pressão inicial. A pressão inicial é a soma da pressão atmosférica com a pressão da coluna de água, isso quer dizer:

Mas antes temos que determinar a massa de água (). O volume de água é dado por:

Olhando na Tabela B.1.1 nas condições de e , temos:

Então a massa é

Substituindo a massa no cálculo da pressão inicial, temos:

Vamos analisar as condições no estado final. No final do processo temos que a água toda foi despejada e temos a pressão atmosférica atuando sobre o pistão:

E o volume final de ar, dado por:

Para o calcula da temperatura final, vamos usar a proporção relacionada a variação da pressão:

Isolando e substituindo os dados, temos:

Com todas as condições de estado definidas, vamos calcular o trabalho.

Nós sabemos que o trabalho é numericamente igual a área sob a curva do diagrama , então vamos dar uma olhada no diagrama:

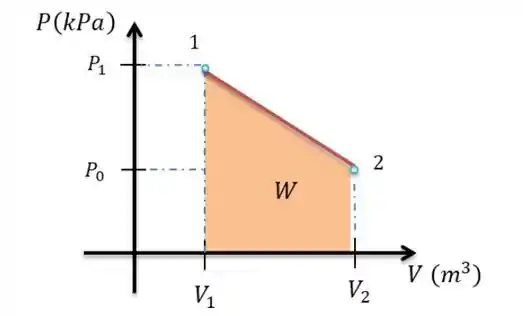
Nós vamos um trapézio, cuja área é dada pela soma das bases dividida por 2 e multiplicada pela altura. Assim,

Finalmente podemos calcular o calor transferido no processo. Utilizando a fórmula do passo 1:

Olhando na Tabela A.5, temos .

Com esse resultado encerramos o exercício 😉.