Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 9.Problemas - Ex. 53

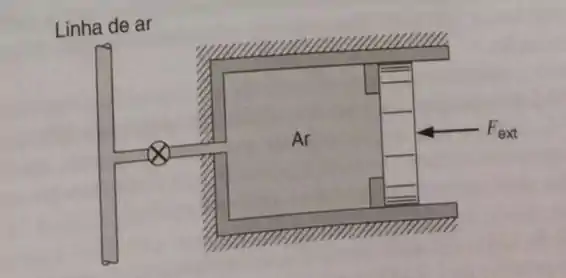
Um cilindro horizontal, termicamente isolado, tem um pistão sem atrito pressionado contra os batentes, por uma força externa de 500   k N , conforme mostrado na Fig. P9.53. A área da seção transversal do pistão é de 0,5   m 2 , e o volume inicial é de 0,25   m 3 . Nesta condição, gás argônio está contido no interior do cilindro a 200   k P a e 100 ° C . Uma válvula é então aberta para uma linha onde escoa argônio a 1,2   M P a e 200 ° C , e o gás flui para dentro do cilindro até que a pressão interna contrabalance a força externa, ponto no qual a válvula é fechada. Use calor específico constante para verificar que a temperatura final é de 645   k J e determine a geração total de entropia.

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Nós temos os seguintes para a substância Argônio, fornecidos pelo enunciado

V = 0,25   m 3

A = 0,2   m 2

F = 500   k N

p 1 = 200   k P a

T 1 = 373,15   K

p i = 1200   k P a

T i = 473,15   K

T 2 = 645   K

Este problema será resolvido usando calores específicos constantes. Da tabela A.5, obteremos a constante do gás e as capacidades de calor específico:

R = 0,2081 k J k g   K

C p 0 = 0,520   k J k g   K

C v 0 = 0,312   k J k g   K

Usando o equilíbrio de forças vamos calcular p 2 :

p 2 A = F

Isolando o p 2

p 2 = F A = 500 0,5 = 1000   k P a

E pela equação da continuidade, nós temos que

m 2 - m 1 = m i

Agora vamos configurar a lei dos gases ideais para os estados 1 e 2 para calcular ambas as massas:

m 1 = p 1 V R T 1

Fazendo a substituição

m 1 = 200 ∙ 0,25 0,2081 ∙ 373,15 = 0,644   k g

Para calcular a massa m 2 , nós precisaremos calcular algumas coisinhas a mais.

Passo 2

No caso de m 2 , nós temos que

m 1 T 1 = p 1 V R

m 2 T 2 = p 2 V R

Vamos configurar a equação de energia para ver o que estamos perdendo:

m i h i = m 2 u 2 - m 1 u 1

Substituindo em m i

m 2 - m 1 h i = m 2 u 2 - m 1 u 1

Desenvolvendo um pouco mais

m 2 - m 1 C p 0 T i = m 2 C v 0 T 2 - m 1 C v 0 T 1

Um pouco mais (é do meme mesmo hehe...)

m 2 - m 1 C p 0 T i = C v 0 ∙ p 2 V - p 1 V R

Logo, temos que

m 2 - m 1 = C v 0 C p 0 T i ∙ p 2 V - p 1 V R

Fazendo a substituição dos termos

m 2 - m 1 = 0,312 0,520 ∙ 473,15 ∙ 0,25 1000 - 200 0,2081 = 1,2187   k g

Agora podemos encontrar a massa no estado 2:

m 2 = 1,2187 + m 1

Com isso,

m 2 = 1,8627   k g

Passo 3

Vamos verificar nossa temperatura final T 3 = 645   K usando a lei dos gases ideais:

T 2 = p 2 V m 2 R

Fazendo a substituição dos termos

T 2 = 1000 ∙ 0,25 1,8627 ∙ 0,2081 = 644,95   K ≈ 645   K

Finalmente, para obter a geração de entropia, temos que configurar a equação de entropia com mudança na entropia da equação e massa de entrada da equação de continuidade:

m 2 s 2 - m 1 s 1 = m i s i + Q T + S g e n

Isolando o S g e n

S g e n = m 1 s i - s 1 + m 2 s 2 - s i - 0

Desenvolvendo um pouco mais as coisas

S g e n = m 1 C p ln ⁡ T i T 1 - R ln ⁡ p i p 1 + m 2 C p ln ⁡ T 2 T i - R ln ⁡ p 2 p i

Fazendo a substituição

S g e n = 0,644 0,520 ∙ ln ⁡ 473,15 373,15 - 0,2081 ∙ ln ⁡ 1200 200 + 1,8627 0,520 ∙ ln ⁡ 64 5 4 73,15 - 0,2081 ∙ ln ⁡ 1 0 00 1 200

Portanto,

S g e n = 0,2102 k J k g

Resposta

T 2 = 645   K

S g e n = 0,2102 k J k g

Exercícios de Livros Relacionados

Um certo processo industrial requer um escoamento permanente de 0,5 k g s de ar a 200m / s , na condição de 150k P a e 300K , conforme mostrado na Fig. P9.71. Esse ar deve ser a exaustão de uma turbin
Calcule a entropia total gerada no processo de enchimento dado no Exemplo 6.11.
R-134a, saturado a - 10 ° C , é bombeado/comprimido até uma pressão de 1,0M P a com uma vazão de 0,5k g / s em um processo adiabático reversível. Calcule a potência requerida e a temperatura de saída
Fluido frigorífico R-12 está contido em um arranjo cilindro-pistão a 2M P a e 150 ° C com um pistão de massa desprezível encostado nos batentes, numa posição em que V = 0,5m 3 . O lado acima do pistão