Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 9.Problemas - Ex. 71

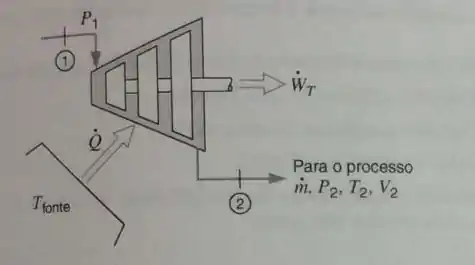
Um certo processo industrial requer um escoamento permanente de 0,5 k g s de ar a 200   m / s , na condição de 150   k P a e 300   K , conforme mostrado na Fig. P9.71. Esse ar deve ser a exaustão de uma turbina, especialmente projetada, cuja pressão de entrada é 400   k P a . O processo na turbina pode ser considerado como reversível e politrópico, com expoente n = 1,20 .

a. Qual é a temperatura de entrada na turbina?

b. Qual é a potência de saída e a taxa de transferência de calor na turbina?

c. Calcule a taxa de aumento líquido de entropia, se a transferência de calor vem de uma fonte a uma temperatura 100 ° C maior do que a temperatura de entrada da turbina?

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

Temos os seguintes dados para turbina reversível com ar:

P 1 = 400   k P a

P 2 = 150   k P a

T 2 = 300   K

v 2 = 200 m s

v 1 = 0

n = 1,2

m ' = 0,5 k g s

T f o n t e = T 1 + 100   K

Com isso, já podemos partir para a resolução da questão, let’s go!

Passo 2

A - Da tabela de propriedades A.5. podemos encontrar o calor específico do ar e a constante do gás:

C p = 1,004 k J k g   K

R = 0,287 k J k g   K

Calculando a temperatura de entrada da turbina:

T 1 = T 2 ∙ P 1 P 2 n - 1 n

Substituindo os termos

T 1 = 300 ∙ 400 150 0,2 1,2 = 353   K

B - Calculando a potência da turbina:

W ' = m ' ∙ R ∙ ( T 2 - T 1 ) 1 - n

Fazendo a substituição dos termos

W ' = 0,5 ∙ 0,287 ∙ 300 - 353 1 - 1,2 = 38   k W

Calculando a taxa de transferência de calor para a turbina:

Q ' = m ' ∙ C p ∙ T 2 - T 1 + W ' + 1 2 m ' ∙ v 2 2 - v 1 2

Novamente, fazendo o processo de substituição

Q ' = 0,5 ∙ 1,004 ∙ 300 - 353 + 38000 + 1 2 ∙ 0,5 ∙ 200 2 - 0

Com isso, nós temos que

Q ' = 21,4   k W

Passo 3

C - A temperatura da fonte é igual a:

T f o n t e = T 1 + 100   K = 453   K

E a geração de entropia é dada por

Δ S g e n = m ' ∙ C p ∙ ln ⁡ T 2 T 1 - m ' ∙ R ∙ ln ⁡ P 2 P 1 - Q ' T f o n t e

Novamente, fazendo o processo de substituir os termos

Δ S g e n = 0,5 ∙ 1,004 ∙ ln ⁡ 300 353 - 0,5 ∙ 0,287 ∙ ln ⁡ 150 400 - 21,4 453

Portanto, nós obtemos o seguinte resultado

Δ S g e n = 0,012 k W K

Resposta

T 1 = 353   K

W ' = 38   k W

Q ' = 21,4   k W

Δ S g e n = 0,012 k W K

Exercícios de Livros Relacionados

Uma pequena bomba recebe água a 20 ° C e 100k P a e descarrega a 2,5M P a com uma vazão de 100k g / m i n . Determine a potência mínima de bombeamento requerida.
Uma pequena bomba d’água no nível do solo tem um tubo de entrada que desce para dentro de um poço com água a 100k P a e 15 ° C e a uma altura H abaixo do nível do solo. A bomba fornece água a 400k P a
Uma pequena bomba, acionada por um motor de 2k W , recebe água líquida a 150k P a e 10 ° C . Determine a vazão máxima que pode ser obtida com uma pressão de saída de 1M P a , desprezando as energias c
Um tanque rígido de 1,0m 3 contém água inicialmente a 120 ° C , com 50 % de líquido e 50% de vapor, em volume. Uma válvula de alívio de pressão, instalada no topo do tanque, é ajustada para 1,0M P a (
Uma mangueira de jardim recebe água líquida a 200k P a e 15 ° C . Qual a velocidade máxima que pode ser gerada em um pequeno bocal ideal? Se você direcionar o bocal diretamente para cima, qual será a